I recently saw a question on a help forum that fits the following pattern. The context is an optimization model (mixed integer program). There is a continuous variable $x$ and a constant value $a$ (frequently but not always 0), and we want to distinguish among three cases (with different consequences in the model): $x<a;$ $x=a;$ or $x>a.$ Each case has separate consequences within the model, which I will call $C_1,$ $C_2$ and $C_3$ respectively. Variations on this question arise frequently. For instance, make $x$ the difference of two variables, set $a=0$ and you are distinguishing whether the difference is negative, zero or positive.
To make things work properly, we need $x$ to be bounded, say $L\le x \le U.$ The goal is to break the feasible range of $x$ into three intervals. To do so, we will introduce a trio of binary variables, $y_1, y_2, y_3$ together with the constraint $$y_1 + y_2 + y_3 = 1.$$ We will come up with constraints such that fixing $y_1 = 1$ puts you in the left portion of the domain, fixing $y_2 = 1$ puts you in the middle portion, and fixing $y_3 = 1$ puts you in the right portion. The $y$ variables are then used elsewhere in the model to enforce whichever condition $C$ applies.
I'm using three variables for clarity. You can get by with two binary variables (changing the equality constraint above to $\le$), where both variables equaling zero defines one of the domain intervals. Figure 1 shows what the user wants and how the $y$ variables relate to it.
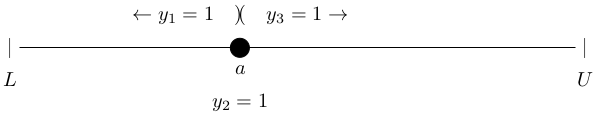 |
| Figure 1 |
The intervals for $x$ are $[L, a)$ when $y_1 = 1$, the singleton $[a, a]$ when $y_2 = 1,$ and $(a, U]$ when $y_3 = 1.$ Unfortunately, the user cannot have what the user wants because the feasible region of a MIP model must be closed, and the first and third intervals in Figure 1 are not closed. Closing them results in Figure 2.
 |
| Figure 2 |
The intervals for $x$ are now $[L, a],$ $[a, a]$ and $[a, U].$ The good news is that this decomposition is easy to accomplish. The bad news is that the user likely will not accept it. If $x=a$, any one of the $y$ variables could take the value 1, so any of the three conditions could be triggered.
This brings us to the first (and more common) of two possible compromises. We can change the strict inequality $x > a$ to the weak inequality $x \ge a + \epsilon$ where $\epsilon$ is some small positive number, and do something analogous with the left interval. The result is Figure 3.
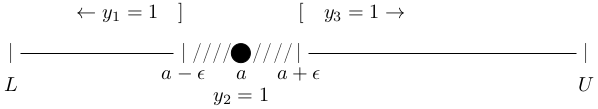 |
| Figure 3 |
Now $y_1=1 \implies x \le a-\epsilon,$ $y_2 = 1 \implies x=a,$ and $y_3=1 \implies x \ge a + \epsilon.$ The good news is that all three intervals are closed. The bad news is that values of $x$ between $a-\epsilon$ and $a$ or between $a$ and $a + \epsilon$ are suddenly infeasible, whereas they were feasible in the original problem. Also note that any tiny deviation from $a$ will throw $x$ into no man's land. That leads to one more possibility, involving yet another positive constant $\delta < \epsilon$ and shown in Figure 4.
 |
| Figure 4 |
The algebra to put either Figure 3 or Figure 4 into force is actually pretty straightforward. You just need to write a pair of inequalities $\dots \le x \le \dots$ where the left side expression is the sum of each $y$ variable times the lower bound that would apply when that variable is 1 and the right expression is the sum of each $y$ variable times the upper bound that would apply. So for Figure 3, where the intervals are $[L, a-\epsilon],$ $[a,a]$ and $[a+\epsilon, U]$, we would have $$Ly_1 + a y_2 + (a+\epsilon)y_3 \le x \le (a-\epsilon)y_1 + a y_2 + Uy_3.$$ For Figure 4, the constraints would be $$Ly_1 + (a-\epsilon+\delta)y_2 + (a+\epsilon)y_3 \le x \le (a-\epsilon)y_1 + (a+\epsilon-\delta) y_2 + Uy_3.$$
There is one "tactical" point to consider. When this is first explained to someone who was unaware that strict inequalities are verboten, they are often tempted to set $\epsilon = 10^{-G}$ where $G$ is the gross domestic product of their native country. The problem is that the solver is using finite precision computer arithmetic, and every solver has a tolerance value $\tau$ (small but not zero) such that coming within $\tau$ of satisfying a constraint is "close enough". If you pick $\epsilon$ (or $\delta$) too small, it has the same consequence as setting it equal to 0 in terms of how valid the solutions are. You can end up with a value of $a$ for $x$ (to within rounding error) triggering consequence $C_1$ or $C_3$ rather than $C_2$, or a value of $x$ strictly greater than $a$ triggering $C_2$ (or possibly even $C_1$), and so on. So $\epsilon$ (and, if needed, $\delta$) must be greater than the rounding tolerance used by the solver.