Guessing Pareto Solutions: A Test

In yesterday's post, I described a simple multiple-criterion decision problem (binary decisions, no constraints), and suggested a possible way to identify a portion of the Pareto frontier using what amounts to guesswork: randomly generate weights; use them to combine the multiple criteria into a single objective function; optimize that (trivial); repeat ad nauseam.

I ran an experiment, just to see whether the idea was a complete dud or not. Before getting into the results, I should manage expectations a bit. Specifically, while it's theoretically possible in some cases that you might find all the Pareto efficient solutions (and is in fact guaranteed if there is only one), in general you should not bank on it. Here's a trivial case that demonstrates that it may be impossible to find them all using my proposed technique. Suppose we have three yes-no decisions ($N=3$, using the notation from yesterday's post) and two criteria ($M=2$), one to be maximized and one to be minimized. Supposed further that, after changing the sign of the second criterion (so that we are maximizing both) and scaling, that all three decisions produce identical criterion values of $(1,-1)$. With $N=3$, there are $2^3=8$ candidate solutions. One (do nothing) produces the result $(0,0)$. Three (do just one thing) produce $(1,-1)$, three (do any two things) produce $(2,-2)$ and one (do all three things) produces $(3,-3)$. All of those are Pareto efficient! However, if we form a weighted combination using weights $(\alpha_1, \alpha_2) \gg 0$ for the criteria, then every decision has the same net impact $\beta = \alpha_1 - \alpha_2$. If $\beta > 0$, the only solution that optimizes the composite function is $x=(1,1,1)$ with value $3\beta$. If $\beta<0$, the only solution that optimizes the composite function is $x=(0,0,0)$ with value $0$. The other six solutions, while Pareto efficient, cannot be found my way.

With that said, I ran a single test using $N=10$ and $M=5$, with randomly generated criterion values. One test like this is not conclusive for all sorts of reasons (including but not limited to the fact that I made the five criteria statistically independent of each other). You can see (and try to reproduce) my work in an R notebook hosted on my web site. The code is embedded in the notebook, and you can extract it easily. Fair warning: it's pretty slow. In particular, I enumerated all the Pareto efficient solutions among the $2^{10} = 1,024$ possible solutions, which took about five minutes on my PC. I then tried one million random weight combinations, which took about four and a half minutes.

Correction: After I rejiggered the code, generating a million random trials took only 5.8 seconds. The bulk of that 4.5 minutes was apparently spent keeping track of how often each solution appeared among the one million results ... and even that dropped to a second or so after I tightened up the code.

To summarize the results, there were 623 Pareto efficient solutions out of the population of 1,024. The random guessing strategy only found 126 of them. It found the heck out of some of them: the maximum number of times the same solution was identified was 203,690! (I guess that one stuck out like a sore thumb.) Finding 126 out of 623 may not sound too good, but bear in mind the idea is to present a decision maker with a reasonable selection of Pareto efficient solutions. I'm not sure how many decision makers would want to see even 126 choices.

A key question is whether the solutions found by the random heuristic are representative of the Pareto frontier. Presented below are scatter plots of four pairs of criteria, showing all the Pareto efficient solutions color-coded according to whether or not they were identified by the heuristic. (You can see higher resolution versions by clicking on the link above to the notebook, which will open in your browser.) In all cases, the upper right corner would be ideal. Are the identified points a representative sample of all the Pareto efficient points? I'll let you judge.

I'll offer one final thought. The weight vectors are drawn uniformly over a unit hypercube of dimension $M$, and the frequency with which each identified Pareto solution occurs within the sample should be proportional to the volume of the region within that hypercube containing weights favoring that solution. So high frequency solutions have those high frequencies because wider ranges of weights favor them. Perhaps that makes them solutions that are more likely to appeal to decision makers than their low frequency (or undiscovered) counterparts?

Guessing Pareto Solutions

One of the challenges of multiple-criteria decision-making (MCDM) is that, in the absence of a definitive weighting or prioritization of criteria, you cannot talk meaningfully about a "best" solution. (Optimization geeks such as myself tend to find that a major turn-off.) Instead, it is common to focus on Pareto efficient solutions. We can say that one solution A dominates another solution B if A does at least as well as B on all criteria and better than B on at least one criterion. A solution is Pareto efficient if no solution dominates it.

Recently I was chatting with a woman about a multiple-criteria model she had. The variables were all binary (yes-no decisions) and were otherwise unconstrained. Normally my hackles would go up at an unconstrained decision problem, but in this case all constraints were "soft". For example, rather than specify a fixed budget, she would make cost one of the criteria (less being better) and let the decision maker screen out Pareto efficient solutions with unrealistic budgets.

I won't name the researcher or go into more details, since her work is currently under review (as of this writing), but I will look at a similar problem that is only slightly simpler. Namely, I will add the requirement that the criteria are additive, meaning that the value of any criterion for any "yes" does not depend on which other decisions wound up "yes" rather than "no". So, in mathematical terms, we have $N$ binary decisions ($x\in\{0,1\}^N$) and $M$ criteria. Let $c_{ij}$ denote the value of criterion $j$ when $x_i=1$. In what follows, I will want to be consistent in maximizing (rather than minimizing) criterion values, so I'll assume that (a) a "no" decision has value 0 for every criterion and (b) criteria are normalized so that $c_{ij}\in [0,1]$ for all $i$ and for all $j$ such that more is better, while $c_{ij}\in [-1,0]$ for all $i$ and for all $j$ such that (before scaling) less is better. For example, if cost is a criterion (and if you do not work for the Pentagon), the scaled values of cost will run from -1 for the most expensive choice encountered to 0 for any choice that is free.

The solution space contains $2^N$ candidate solutions, which means that enumerating them is out of the question for nontrivial values of $N$ (and, trust me, hers are nontrivial ... very, very nontrivial). In any case, the size of the Pareto frontier when $N$ is nontrivial will quickly outpace any decision maker's capacity (or patience). So it seems reasonable to sample the Pareto frontier and present the solution maker with a reasonably (but not excessively) large set of Pareto efficient solutions that hopefully is representative of the overall Pareto frontier.

There are methods for doing this, and the researcher pointed me toward one: the NSGA-II genetic algorithm [1]. Like any genetic algorithm, NSGA-II runs until you stop it via some limit (run time, number of generations, some measure of stagnation, ...). As I understand it, the final population of solutions are not guaranteed to be Pareto efficient, but the population converges in some sense to the Pareto frontier. That would likely be sufficient in practice, and the researcher had good luck with it initially, but ran into scaling problems as $N$ grew.

Looking at the problem reminded me of a sometimes troubling dichotomy faced by academics (in at least some disciplines, including operations research). On the one hand, real-world decision makers with real-world problems are often quite happy to get solutions that are obtained quickly and cheaply and are easily explained or understood, even if the technology is "primitive". Academics, on the other hand, usually need to publish their research. In the domain of the problem, low-tech algorithms may be perfectly fine (and easier to understand than more esoteric algorithms), but for a professor in IE or OR looking to publish in a journal in his or her field, "simple" usually means "too unsophisticated to publish". Thus we tend at times to "over-engineer" solutions.

Anyway, taking off my academic hat for a moment, I got to wondering whether a no-brainer random search approach would work for a problem such as this one. My premise was the following. Suppose I randomly select weights $\alpha_1,\dots,\alpha_M \in (0,1]$ and use them to form a single weighted criterion function $f_\alpha:\{0,1\}^N \rightarrow \Re$ as follows:$$f_\alpha (x)=\sum_{i=1}^N w_i(\alpha) x_i$$where$$w_i(\alpha)=\sum_{j=1}^M \alpha_j c_{ij}.$$Note that the weights $\alpha_i$ need to be strictly positive, not just nonnegative. Maximizing $f_\alpha$ over the solution space is trivial: set $x_i=1$ if $w_i(\alpha) > 0$ and $x_i=0$ if $w_i(\alpha) < 0$. (You can set $x_i$ to anything you like if $w_i(\alpha) = 0$, but that should have probability 0 of occurring given the random generation of $\alpha$.) Constructing the coefficients of $f_\alpha$ is $O(MN)$ and optimizing $f_\alpha$ is $O(N)$, so each solution $x$ produced this way takes $O(MN)$ time. In practice, $M$ is likely not to get too big, and very likely does not grow as $N$ does, so functionally this is really $O(N)$ in complexity.

It's trivial to show that, so long as none of the composite weights $w_i(\alpha)$ is 0, each $x$ found by optimizing some $f_\alpha$ must be Pareto efficient. So we can generate a sample of Pareto efficient solutions fairly efficiently ... maybe. I did deal one card off the bottom of the deck. Solutions will tend to repeat, so we will need to do some bookkeeping to ensure that, in the final results, duplicates are weeded out. That means comparing each new solution to its predecessors. Each comparison is $O(N)$, and if we assume that we only retain a "reasonable" number of alternatives (a number that does not grow with $N$) in order to avoid causing the decision maker's brain to explode, then time spent weeding duplicates should be $O(N)$. Overall, the load is $O(NR)$, where $R$ is the number of replications performed.

That left me with a few questions, the main one being this: for plausible sample sizes, how well does the set of solutions obtained represent the Pareto frontier? Is it "biased" in the sense that solutions cluster on one part of the frontier while missing other parts?

I'll show some experimental results in my next post, and let you decide.


[1] K. Deb, A. Pratap, S. Agarwal & T. Meyarivan (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6, 182-197.

Coin Flipping

I don't recall the details, but in a group conversation recently someone brought up the fact that if you flip a fair coin repeatedly until you encounter a particular pattern, the expected number of tosses needed to get HH is greater than the expected number to get HT (H and T denoting head and tail respectively). Not long after that conversation, I read a reference to the same issue in a blog post.

There's a bit of confusion around this, and I think it has to do with the experiment not being clearly posed. In this post, I will exhaust all options (and likely all readers). Before diving into variations, I will make two standing assumptions regarding the tossing of a pair of coins. The first is that the coins are distinguishable (there is a first coin and a second coin), so that HT and TH are distinct outcomes. The second is that if the "game" ends due to the result of the first of the two coins, the second coin still counts as a toss. To give a concrete example, suppose that we toss our pair of coins twice, looking for two consecutive heads, and observe the following: TH, HT. The first coin in the second toss completed the target sequence (HH), but we will still count this as a total of four coin flips rather than calling it three (ignoring the final T).

The key difference among variations in this "game" will be memory: do prior outcomes affect the chances of "winning" (finding the target pattern) in the next attempt? Let's start with totally independent trials.

Independent Trials

I flip two coins (or one coin twice), and either find my pattern or not. If I do not find my pattern, I erase any record of what pattern I did find and try again.

Under these rules, the number of failed attempts ("attempt" meaning two coin flips, either sequential or simultaneous) until the target is found follows a negative binomial distribution. Unfortunately, the Wikipedia entry defines this in terms of the number of successes until a specified number of failures, which is the reverse of our viewpoint. So we will temporarily define not finding the target pattern as a "success" and finding the target pattern as a "failure". Regardless of whether the target is HH or HT, there is a 0.25 probability of any attempt being a "failure". Since we stop on the first "failure", the expected number of "successes" is $$\frac{p}{1-p} = \frac{0.75}{1-0.75} = 3.$$In the notation of the Wikipedia entry, $r=1$ is the number of "failures" (times we find the target)  needed to stop the process and $p=0.75$ is the probability of "success" (not finding the target) on a single pair of tosses. The key takeaway is that both HH and HT have an expectation of three non-matches before the first match, or four attempts total to get a match. (Reminder: This is an expected value. Your mileage may vary.)

Dependent Trials

Now let's change the game by remembering the last result we got, with an option to include it in the pattern. In this version, tossing one coin repeatedly versus tossing a pair a coins will differ, so I'll start with a single coin. To illustrate the change, suppose our target pattern is HH and our first two tosses result in TH. Previously, we had to start from scratch, and only HH on our next two tosses would win. Now we can win with HT as well, since the second and third tosses combine to make the pattern: TH | HT. This also illustrates the difference between tossing a single coin repeatedly versus a pair of coins. With a pair of coins, that would count as four tosses; with a single coin, we would stop on the second H (three tosses) and never see that final T. (Tossing a single coin but requiring an even number of tosses is no different than tossing a pair of coins.)

Flipping One Coin

We can model our single toss process as a stationary (discrete-time) Markov chain. The state of the system will be the last result we saw: H, T or D (meaning "done"). State D is an absorbing state: when you're done, you're done forever. The game has the "memoryless" property that only the current state (most recent single coin flip) has any effect on what happens next. The transition probability matrix (row = current state, column = next state) looks like this:

	H	T	D
H	0	0.5	0.5
T	0.5	0.5	0
D	0	0	1

We have neither a head nor tail at the outset, which is functionally equivalent to starting in state T: it will take a minimum of two tosses to "win". The quantity we seek is known as the expected first passage time from state T (start) to state D (done). Sadly, the Wikipedia entry skips over first passage times, and a Google search found lots of PDFs and one video but no helpful web pages. Key fact: if $p_{ij}$ denotes the transition probability from state $i$ to state $j$ and $F_{ij}$ denotes the first passage time from $i$ to $j$ (the number of transitions required, starting in state $i$, until state $j$ is first encountered), then for $i\neq j$\[ E[F_{ij}]=1+\sum_{k\neq j}p_{ik}E[F_{kj}]. \]I'm deliberately glossing over a bunch of stuff (transient versus recurrent states, communicating classes, ...). You can read up on it if you don't trust me.

If we solve these equations using the above matrix (reminder: HH is the target), we get $$E[F_{TD}] = 6$$(and  $E[F_{HD}] = 4$).

Next, let's change the target pattern from HH to HT. This changes the transition matrix to:

	H	T	D
H	0.5	0	0.5
T	0.5	0.5	0
D	0	0	1

Solve for first passage times using the revised matrix, and we get $$E[F_{TD}] = 4$$(and $E[F_{HD}]=2$).

Conclusion: Tossing one coin continuously, we need an average of four tosses to find HT but an average of six to find HH.

Flipping a Pair of Coins

Now suppose we flip two coins at a time. Again, we start with HH as the target. Our transition probability matrix is now the following:

	H	T	D
H	0.25	0.25	0.5
T	0.25	0.5	0.25
D	0	0	1

To clarify the transition probabilities, if my last toss (of two coins) ended with a head, HH or HT gives me a "win", TH keeps me in state H, and TT sends me to state T. If my last toss ended in a tail, HH gives me a "win", HT or TT keeps me in state T, and TH sends me to state H. The expected first passage time T to D is $$E[F_{TD}] = 3.2;$$but since each transition involves tossing two coins, that means I need an average of 6.4 tosses to win. That slightly exceeds the 6 we had for the single coin version, which makes sense; we "waste" some tosses when the first coin completes the pattern and the second coin proves unnecessary.

For the HT target, the transition probability matrix is:

	H	T	D
H	0.25	0	0.75
T	0.5	0.25	0.25
D	0	0	1

From state H, HT, TH and TT are all "wins", while HH keeps me in state H. From state T, only HT is a "win"; HH and TH send me to state H, and TT keeps me in state T. We find$$E[F_{TD}] = \frac{20}{9} = 2.2222...$$and so an average of 4.444... coin tosses are needed to find the HT pattern.

Which pretty much pounded the daylights out of that subject. :-) If you want to experiment with this, I've posted some R code (which uses the markovchain library package).

Histogram Abuse

Consider the following Trellis display of histograms of a response variable ($Z$), conditioned on two factors $(X, Y)$ that can each be low, medium or high:

The combined sample size for the nine plots is 10,000 observations. Would you agree with the following assessments?

• $Z$ seems to be normally distributed for medium values of either $X$ or $Y$ (or both).
• $Z$ appears to be negatively skewed when both $X$ and $Y$ are low (and perhaps when $X$ is low and $Y$ is high), and perhaps positively skewed when both $X$ and $Y$ are high.
• $Z$ appears to be leptokurtic when both $X$ and $Y$ are low.

What motivated this post is a video I recently watched, in which the presenter generated a matrix of conditional histograms similar to this one. In fairness to the presenter (whom I shall not name), the purpose of the video was to show how to code plots like this one, not to do actual statistical analysis. In presenting the end result, he made some off-hand remarks about distributional differences of the response variable across various values of the covariates. Those remarks caused my brain to itch.

So, are my bulleted statements correct? Only the first one, and that only partially. (The reference to $Y$ is spurious.) In actuality, $Z$ is independent of $Y$, and its conditional distribution given any value of $X$ is normal (mesokurtic, no skew). More precisely, $Z=2X+U$ where $U\sim N(0,1)$ is independent of both $X$ and $Y$. The data is simulated, so I can say this with some assurance.

If you bought into any of the bulleted statements (including the "either-or" in the first one), where did you go wrong? It's tempting to blame the software's choice of endpoints for the bars in the histograms, since it's well known that changing the endpoints in a histogram can significantly alter its appearance, but that may be a bit facile. I used the lattice package in R to generate the plot (and those below), and I imagine some effort went into the coding of the default endpoint choices in the histogram() function. Here are other things to ponder.

Drawing something does not make it real.

The presence of $Y$ in the plots tempts one to assume that it is related to $Z$, even without sufficient context to justify that assumption.

Sample size matters.

The first thing that made my brain itch, when I watched the aforementioned video, was that I did not know how the covariates related to each other. That may affect the histograms, particularly in terms of sample size.

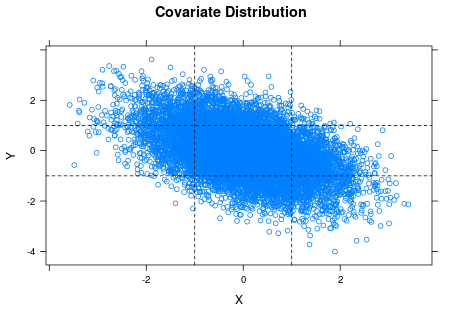
It is common knowledge that the accuracy of histograms (and pretty much everything else statistical) improves when sample size increases. The kicker here is that we should ask about the sample sizes of the individual plots. It turns out that $X$ and $Y$ are fairly strongly correlated (because I made them so). We have 10,000 observations stretched across nine histograms. An average of over 1,000 observations per histogram should be enough to get reasonable accuracy, but we do not actually have 1,000 data points in every histogram. The scatter plot of the original covariates (before turning them into low/medium/high factors) is instructive.

The horizontal and vertical lines are the cuts for classifying $X$ and $Y$ as low, medium or high. You can see the strong negative correlation between $X$ and $Y$ in the plot. If you look at the lower left and upper right rectangles, you can also see that the samples for the corresponding two histograms of $Z$ ($X$ and $Y$ both low or both high) are pretty thin, which suggests we should not trust those histograms so much.

Factors often hide variation (in arbitrary ways).

In some cases, factors represent something inherently discrete (such as gender), but in other cases they are used to categorize (pool) values of a more granular variable. In this case, I cut the original numeric covariates into factors using the intervals $(-\infty, -1]$, $(-1, +1]$ and $(+1, +\infty)$. Since both covariates are standard normal, that should put approximately 2/3 of the observations of each in the "medium" category, with approximately 1/6 each in "low" and "high".

To generate the plot matrix, I must convert $X$ and $Y$ to factors; I cannot produce a histogram for each individual value of $X$ (let alone each combination of $X$ and $Y$). Even if my sample were large enough that each histogram had sufficiently many points, the reader would drown in that many plots. Using factors, however, means implicitly treating $X=-0.7$ and $X=+0.3$ as the same ("medium") when it comes to $Z$. This leads to the next issue (my second "brain itch" when viewing the video).

Mixing distributions blurs things.

As noted above, in the original lattice of histograms I am treating the conditional distributions of $Z$ for all $(X, Y)$ values in a particular category as identical, which they are not. When you mix observations from different distributions, even if they come from the same family (normal in this case) and have only modestly different parameterizations, you end up with a histogram of a steaming mess. Here the conditional distribution of $Z$ given $X=x$ is $N(2x, 1)$, so means are close if $X$ values are close and standard deviations are constant. Nonetheless, I have no particular reason to expect a sample of $Z$ when $X$ varies between $-1$ and $+1$ to be normal, let alone a sample where $X$ varies between $-\infty$ and $-1$.

To illustrate this point, let me shift gears a bit. Here is a matrix of histograms from samples of nine variables $X_1,\dots,X_9$ where $X_k \sim N(k, 1)$.

Each sample has size 100. I have superimposed the normal density function on each plot. I would say that every one of the subsamples looks plausibly normal.

Now suppose that there is actually a single variable $X$ whose distribution depends on which of the nine values of $k$ is chosen. In order to discuss the marginal distribution of $X$, I'll assume that an arbitrary observation comes from a random choice of $k$. (Trying to define "marginal distribution" when the distribution is conditioned on something deterministic is a misadventure for another day.) As an example, $k$ might represent one of nine possible categories for undergraduate major, and $X$ might be average annual salary over an individual's working career.

Let's see what happens when I dump the 900 observations into a single sample and produce a histogram.

The wobbly black curve is a sample estimate of the density function, and the red curve is the normal density with mean and standard deviation equaling those of the sample (i.e., $\mu=\bar{X}, \sigma=S_X$). To me, the sample distribution looks reasonably symmetric but too platykurtic (wide, flat) to be normal ... which is fine, because I don't think the marginal distribution of $X$ is likely to be normal. It will be some convolution of the conditional distribution of $X$ given $k$ (normal, with mean $k$) with the probability distribution for $k$ ... in other words, a steaming mess.

When we pool observations of $X$ from different values of $k$, we are in effect mixing apples and oranges. This is what I meant by "blurring" things. The same thing went on in the original plot matrix, where we treated values of $Z$ coming from different distributions (different values of $X$ in a single category, such as "medium") as being from a common distribution.

So what is the takeaway here?

In Empirical Model Building and Response Surfaces (Box and Draper, 1987), the following quote appears, usually attributed to George E. P. Box: "Essentially, all models are wrong, but some are useful." I think that the same can be said about statistical graphs, but perhaps should be worded more strongly. Besides visual appeal, graphics often make the viewer feel that they are what they are seeing is credible (particularly if the images are well-organized and of good quality) and easy to understand. The seductive feeling that you are seeing something "obvious" makes them dangerous.

Anyone who is curious (or suspicious) is welcome to download my R code.

The White Knight Returns

Back in May, on his excellent blog The Endeavor, John D. Cook posed (and subsequently answered) the following problem: if a knight begins in one corner of an empty chessboard and moves randomly, each time choosing uniformly over the available moves from its current position, what is the mean number of moves until it returns to the corner from which it started?

Several people posed exact or approximate answers in the comments. The approximate answers were based on simulation. The most elegant solution among the comments, posted by 'deinst', modeled the problem as a reversible Markov chain on a graph. John Cook's answer used a rather powerful theorem about a random walk on a graph, which I think boils down to the same logic used by 'deinst'. (Cook also includes Python code for a simulation.)

When I read the problem, my first reaction was also to model it as a Markov chain, but sadly I've forgotten most of what I knew about MC's, including the concept of reversibility. I did, at least, recall the essentials of first passage time. The question reduces to computing the expected first passage time from the corner square to itself. The Wikipedia link for first passage times is not entirely helpful, as it is not specific to Markov chains, but the concept is easy to explain. Let the corner in which the knight starts be position $s$, and let $\mu_j$ denote the expected number of moves required until the knight first returns to position $s$, given that it is currently at position $j$ (i.e., the expected first passage time from $j$ to $s$). The answer to the puzzle is $\mu_s$, the expected first passage time from $s$ to itself. Further, let $M_j$ denote the set of positions that the knight can reach in one move, given that it is currently at position $j$. Letting $p_{jk}$ denote the probability that a knight at position $j$ next moves to position $k$, the first passage times $\mu_\cdot$ satisfy the following system of linear equations:\[ \mu_{j}=1+\sum_{k\in M_{j}\backslash\{s\}}p_{jk}\mu_{k}\quad\forall j. \] In our case, $p_{jk} = 1/|M_j|$ if $k\in M_j$ and 0 otherwise. The solution to this system has $\mu_s=168$ (matching the answers of John Cook and deinst).

Other than a quick refresher on Markov chains, my main interest in this was that I'm teaching myself Python while also trying to get a handle on using Sage. So I wrote a Sage notebook to set up and solve the first passage time equations. Here is the content of that notebook, in case anyone is curious. (Please bear in mind I'm new to Python.)

Define the board

board = [(i, j) for i in range(8) for j in range(8)]

Assign a variable for the expected first passage time (to the lower left corner) from each square of the board

vlist = {b : var('r_' + str(b[0]) + '_' + str(b[1])) for b in board}

List the eight moves a knight can make

moves = [(i, j) for i in [-2, -1, 1, 2] for j in [-2, -1, 1, 2] if abs(i) + abs(j) == 3]

Define a function that takes a position and move and returns the new position if the move is legal, None otherwise

def move(position, change): 

    if (position in board) and (change in moves): 

        landing = (position[0] + change[0], position[1] + change[1])

        return landing if landing in board else None

    else:

        return None

Compute all legal moves from each board position

legal = {p : [move(p, m) for m in moves if not(move(p, m) is None)] for p in board}

Set up the first passage time equations

eqns = [vlist[b] == 1.0 + (1.0/len(legal[b]))*sum([vlist[x] for x in legal[b] if x != (0, 0)]) for b in board]

Solve the equations

sols = solve(eqns, vlist.values(), solution_dict = True)

Verify that the solution is unique

len(sols) == 1

True

Find the mean first passage time from position (0,0) to itself

sols[0][vlist[(0,0)]]

168

One last note: I had originally intended to give the post a Christian Bale buzz by titling it "The Dark Night Returns". Turns out DC Comics beat me to that title. Oh, well.