For quite a while, I was getting security nags from Firefox every time a web site wanted to run a Java applet. Firefox would tell me I needed to upgrade to the latest version of Java. That would have been fine, except that I was already running the latest Java (1.8.0_66 as of this writing). I manually downloaded and installed the SDK (which includes the JRE). So apparently there was something about the installation that was confusing Firefox into using an earlier version (?).
Anyway, long story short, I found a PPA from the ever helpful folks at Web Upd8 that makes it easy to get the installation correct, at least on Ubuntu and derivatives (including Mint). The PPA installs a package that downloads the binaries from Oracle, installs them, makes them the defaults etc.
On an unrelated note, this was not the post I started to write. I enter the math notation in this blog in LaTeX and rely on MathJax to translate it to MathML for browsers that understand MathML (Firefox being one). I noticed a week or so ago when viewing an old post that Firefox was inserting copious unnecessary (and unwanted) vertical space on either side of any line containing math, whether the math was "inline" or "display mode". Horizontal spacing was fine; only vertical spacing was munged. Checking around, I found that (a) it was happening on every page with MathJax content, not just on my blog, (b) it depended to some extent on which font was being used (with the XITS font, no extra space was inserted), and (c) Google Chrome was unaffected. So it appeared to be something involving the combination of Firefox and specific fonts. I did some research on Firefox extensions and was literally half way through typing up a post with a solution when, by chance, I discovered that the problem apparently went away. I don't know what changed, but suddenly Firefox is getting the vertical spacing correct again.
So my new tool for all technical problems is to write half a blog post about them and then see if that is enough to cure the problems. :-)
Tuesday, December 29, 2015
Sunday, November 22, 2015
On Statistics, Reporting and Bacon
I've previously ranted about the need for a "journalistic analytics" college major, to help with reporting (and editing) news containing statistical analysis. Today I read an otherwise well written article that inadvertently demonstrates how easy it is for even seasoned reporters to slip up.
The cover story of the November 9 issue of Time magazine, written by Jeffrey Kluger, has the title "Red Meat, Hot Dogs and the War on Delicious". It's main focus is a recent meta-analysis that found links between consumption of meat (and particularly processed meat) and colorectal cancer. As a Time subscriber, I've read quite a few articles by Mr. Kluger, who covers the "science beat" for them, and I have a great deal of respect for his ability to interpret scientific evidence and present it both accurately and interestingly. So I was a bit bemused to encounter the following paragraph (approximately midway through the article):
I don't want to belabor this, nor to find fault with Mr. Kluger (or his editor and/or fact-checker). It's just evidence that even seasoned reporters can commit an occasional statistical faux pas when the flow of the narrative grips them.
The cover story of the November 9 issue of Time magazine, written by Jeffrey Kluger, has the title "Red Meat, Hot Dogs and the War on Delicious". It's main focus is a recent meta-analysis that found links between consumption of meat (and particularly processed meat) and colorectal cancer. As a Time subscriber, I've read quite a few articles by Mr. Kluger, who covers the "science beat" for them, and I have a great deal of respect for his ability to interpret scientific evidence and present it both accurately and interestingly. So I was a bit bemused to encounter the following paragraph (approximately midway through the article):
Figures like that are not always easy to understand and can be more alarming than they need to be. The lifetime risk for developing colorectal cancer is just 5% for men and a little lower for women. A hot dog a day would raise that risk by 18% of the 5%–topping you out at about a 6% overall risk. But that assumes that’s all the red meat you ever eat, and those 1% increments add up fast.Unless the lifetime risk statistics are for confirmed vegetarians (which I doubt), the rise from 5% to 6% lifetime risk would be caused by one hot dog a day (or equivalent) added to your normal diet. Presuming the morbidity statistics were for US citizens (the core audience for Time, I assume), we can put this in the context of a statistic from an earlier paragraph:
In 2013, the average American consumed more than 71 lb. of beef, lamb, veal and pork ...I'm pretty sure that 71 lb. per person excludes "turkey bacon" and possibly a few other meats that, while not technically "red meats", were found to contain the same nitrates and nitrites that were associated with cancer risk in the meta-study. So the "normal diet" to which you're adding that incremental hot dog per day (or equivalent, for those of you who don't really want an extra hot dog every day) is not exactly devoid of meat products. Therefore, "[b]ut that assumes that's all the read meat you ever eat" is incorrect. (According to my scale, "those 1% increments add up fast" is indeed accurate.)
I don't want to belabor this, nor to find fault with Mr. Kluger (or his editor and/or fact-checker). It's just evidence that even seasoned reporters can commit an occasional statistical faux pas when the flow of the narrative grips them.
| source: http://www.funniestmemes.com/funny-memes-low-carb-and-gluten-free-salad/ |
Wednesday, October 21, 2015
Regression Via Pseudoinverse
In my last post (OLS Oddities), I mentioned that OLS linear regression could be done with multicollinear data using the Moore-Penrose pseudoinverse. I want to tidy up one small loose end.
Specifically, let $X$ be the matrix of predictor observations (including a column of ones if a constant term is desired), let $y$ be a vector of observations of the dependent variable, and suppose that you want to fit the model $y = X\beta + \epsilon$ where $\epsilon$ is the noise term and $\beta$ the coefficient vector. The normal equations $$b = \left(X^\prime X\right)^{-1}X^\prime y$$produce the least squares estimate of $\beta$ when $X$ has full column rank. If we let $M^+$ denote the Moore-Penrose pseudoinverse of matrix $M$ (which always exists and is unique), then $$\hat{b} = X^+ y$$results in $\hat{y} = X\hat{b}$ giving the correct fitted values even when $X$ has less than full rank (i.e., when the predictors are multicollinear).
What if you replace the inverse with a pseudoinverse in the normal equations? In other words, suppose we let $$\tilde{b} = \left(X^\prime X\right)^+X^\prime y.$$Do we get the same fitted values $\hat{y}$?
We do, and in fact $\tilde{b} = \hat{b}$, i.e., both ways of using the pseudoinverse produce the same coefficient vector. The reason is that $$\left(X^\prime X\right)^+X^\prime = X^+.$$A proof is given in section 4.2 of the Wikipedia page of "Proofs involving the Moore-Penrose pseudoinverse", so I won't bother to reproduce it here.
If $X$ is $m \times n$, the second approach will be preferable only if the computational cost of finding the pseudoinverse of the $n \times n$ matrix $X^\prime X$ is sufficiently less than the cost of finding the pseudoinverse of $X$ to offset the $O\left(mn^2\right)$ cost of the multiplication of $X^\prime$ and $X$. I don't know if that's true, particularly in some machine learning applications where, apparently, $n >> m$. So I'll either stick to the simpler version (using $X^+$) or, more likely, continue with the time-honored tradition of weeding out redundant predictors before fitting the model.
Specifically, let $X$ be the matrix of predictor observations (including a column of ones if a constant term is desired), let $y$ be a vector of observations of the dependent variable, and suppose that you want to fit the model $y = X\beta + \epsilon$ where $\epsilon$ is the noise term and $\beta$ the coefficient vector. The normal equations $$b = \left(X^\prime X\right)^{-1}X^\prime y$$produce the least squares estimate of $\beta$ when $X$ has full column rank. If we let $M^+$ denote the Moore-Penrose pseudoinverse of matrix $M$ (which always exists and is unique), then $$\hat{b} = X^+ y$$results in $\hat{y} = X\hat{b}$ giving the correct fitted values even when $X$ has less than full rank (i.e., when the predictors are multicollinear).
What if you replace the inverse with a pseudoinverse in the normal equations? In other words, suppose we let $$\tilde{b} = \left(X^\prime X\right)^+X^\prime y.$$Do we get the same fitted values $\hat{y}$?
We do, and in fact $\tilde{b} = \hat{b}$, i.e., both ways of using the pseudoinverse produce the same coefficient vector. The reason is that $$\left(X^\prime X\right)^+X^\prime = X^+.$$A proof is given in section 4.2 of the Wikipedia page of "Proofs involving the Moore-Penrose pseudoinverse", so I won't bother to reproduce it here.
If $X$ is $m \times n$, the second approach will be preferable only if the computational cost of finding the pseudoinverse of the $n \times n$ matrix $X^\prime X$ is sufficiently less than the cost of finding the pseudoinverse of $X$ to offset the $O\left(mn^2\right)$ cost of the multiplication of $X^\prime$ and $X$. I don't know if that's true, particularly in some machine learning applications where, apparently, $n >> m$. So I'll either stick to the simpler version (using $X^+$) or, more likely, continue with the time-honored tradition of weeding out redundant predictors before fitting the model.
Sunday, October 18, 2015
OLS Oddities
During a couple of the lectures in the Machine Learning MOOC offered by Prof. Andrew Ng of Stanford University, I came across two statements about ordinary least squares linear regression (henceforth OLS) that surprised me. Given that I taught regression for years, I was surprised that I could be surprised (meta-surprised?), but these two facts are not ones you're likely to see in a statistics course.
The first is not too shocking in hindsight. Let $X$ be an $m \times n$ matrix containing $m$ observations of $n$ predictors (including a column of ones if you want a constant term in the model) and let $y$ be an $m \times 1$ vector of observations of the dependent variable. A linear model looks like $$y = Xb + e$$where $b$ is the estimated coefficient vector ($n \times 1$) and $e$ is the vector of residuals ($m \times 1$). By definition OLS computes $b$ to minimize the sum of squared residuals $$J(b) = e^\prime e.$$The so-called normal equations are derived by computing the gradient of $J$ and setting it equal to zero. Assuming $X$ has full column rank, this yields $$b = (X^\prime X)^{-1}X^\prime y.$$ Surprising (to me) fact #1: when dealing with large data sets, you may not want to use the nice, closed form, normal equations to compute $b$. The alternative is an iterative approach, using a nonlinear programming algorithm such as gradient descent, or the conjugate gradient method, or some other alternative. The reason is that $(X^\prime X)^{-1}$ may be computationally expensive to compute when $m$ and particularly $n$ are large. In practice, good statistical software would not invert the matrix anyway; it would do some sort of decomposition (LU, decomposition, whatever) both for efficiency and to head off potential rounding problems. Apparently, though, the comparatively small amount of arithmetic required per iteration of gradient descent (mainly computing $X b$ and $X^\prime e$, which are $O(mn)$ operations) offsets the cost of running a bunch of iterations rather doing a one-and-done solution of a matrix equation.
The bigger surprise, though, had to do with multicollinearity, which occurs when $X$ has less than full column rank. Multicollinearity means $X^\prime X$ is singular and cannot be inverted. It also means the model contains redundant predictors (some predictors are linear combinations of others), and I always gave my students the standard prescription: figure out which predictors were redundant and eliminate them. Other people sometimes recommend a perturbation approach (ridge regression). For that matter, gradient descent should work properly with multicollinear data.
Before continuing, I need to inject a well-established if not necessarily well-known fact about multicollinearity. Whether $X$ is multicollinear or not, there is a unique vector $\hat{y}$ of fitted values that minimizes the sum of squared errors. This is because $\hat{y}$ is the orthogonal projection of $y$ onto the column space of $X$, and the orthogonal project of any vector onto any linear subspace is unique. When $X$ has full rank, $\hat{y} =Xb$ where $b$ is given by the normal equations (and is the unique coefficient vector that generates $\hat{y}$. When $X$ is less than full rank (multicollinear), the optimal fitted values $\hat{y}$ can be obtained from any of an infinite number of coefficient vectors ... but the fits are still uniquely determined.
The big surprise for me: it turns out that you can fit a version of the normal equations using the Moore-Penrose pseudoinverse of $X$. I'd come across the pseudoinverse in some long ago linear algebra or numerical analysis class, filed it away as another mathematical curiosity of no particular use, and forgotten it. Oops.
Let $A$ be the pseudoinverse of $X$ (which always exists, is unique, and has dimensions $n \times m$). Then $\hat{b} = Ay$ yields the correct fitted values $X \hat{b}$. A proof begins with one of the identities true of the pseudoinverse: $$X^\prime = X^\prime X A.$$Now the gradient $\nabla_b J(b)$ works out to $-2X^\prime e$; substitute $y - XAy$ for $e$ and $\hat{b}$ for $b$, and we have \begin{alignat*}{1} \nabla_{b}J(\hat{b}) & =-2X^{\prime}e\\ & =-2X^{\prime}\left(y-X\hat{b}\right)\\ & =-2X^{\prime}\left(y-XAy\right)\\ & =-2X^{\prime}(I-XA)y\\ & =-2\left(X^{\prime}-X^{\prime}XA\right)y. \end{alignat*}Substitute the aforementioned identity for the middle expression and we have $ \nabla_{b}J(\hat{b}) = 0$. So choosing $b=\hat{b}$ minimizes squared errors and thus gives the proper fitted values.
All that said, I would still rather eliminate redundant predictors. That process can be automated, but if you are writing a machine learning algorithm that will chew through potentially large data sets with no human supervision, and you want to use linear (or polynomial) models, I suppose you should at least consider using the entire data set with the pseudoinverse taking care of the multicollinearity.
The first is not too shocking in hindsight. Let $X$ be an $m \times n$ matrix containing $m$ observations of $n$ predictors (including a column of ones if you want a constant term in the model) and let $y$ be an $m \times 1$ vector of observations of the dependent variable. A linear model looks like $$y = Xb + e$$where $b$ is the estimated coefficient vector ($n \times 1$) and $e$ is the vector of residuals ($m \times 1$). By definition OLS computes $b$ to minimize the sum of squared residuals $$J(b) = e^\prime e.$$The so-called normal equations are derived by computing the gradient of $J$ and setting it equal to zero. Assuming $X$ has full column rank, this yields $$b = (X^\prime X)^{-1}X^\prime y.$$ Surprising (to me) fact #1: when dealing with large data sets, you may not want to use the nice, closed form, normal equations to compute $b$. The alternative is an iterative approach, using a nonlinear programming algorithm such as gradient descent, or the conjugate gradient method, or some other alternative. The reason is that $(X^\prime X)^{-1}$ may be computationally expensive to compute when $m$ and particularly $n$ are large. In practice, good statistical software would not invert the matrix anyway; it would do some sort of decomposition (LU, decomposition, whatever) both for efficiency and to head off potential rounding problems. Apparently, though, the comparatively small amount of arithmetic required per iteration of gradient descent (mainly computing $X b$ and $X^\prime e$, which are $O(mn)$ operations) offsets the cost of running a bunch of iterations rather doing a one-and-done solution of a matrix equation.
The bigger surprise, though, had to do with multicollinearity, which occurs when $X$ has less than full column rank. Multicollinearity means $X^\prime X$ is singular and cannot be inverted. It also means the model contains redundant predictors (some predictors are linear combinations of others), and I always gave my students the standard prescription: figure out which predictors were redundant and eliminate them. Other people sometimes recommend a perturbation approach (ridge regression). For that matter, gradient descent should work properly with multicollinear data.
Before continuing, I need to inject a well-established if not necessarily well-known fact about multicollinearity. Whether $X$ is multicollinear or not, there is a unique vector $\hat{y}$ of fitted values that minimizes the sum of squared errors. This is because $\hat{y}$ is the orthogonal projection of $y$ onto the column space of $X$, and the orthogonal project of any vector onto any linear subspace is unique. When $X$ has full rank, $\hat{y} =Xb$ where $b$ is given by the normal equations (and is the unique coefficient vector that generates $\hat{y}$. When $X$ is less than full rank (multicollinear), the optimal fitted values $\hat{y}$ can be obtained from any of an infinite number of coefficient vectors ... but the fits are still uniquely determined.
The big surprise for me: it turns out that you can fit a version of the normal equations using the Moore-Penrose pseudoinverse of $X$. I'd come across the pseudoinverse in some long ago linear algebra or numerical analysis class, filed it away as another mathematical curiosity of no particular use, and forgotten it. Oops.
Let $A$ be the pseudoinverse of $X$ (which always exists, is unique, and has dimensions $n \times m$). Then $\hat{b} = Ay$ yields the correct fitted values $X \hat{b}$. A proof begins with one of the identities true of the pseudoinverse: $$X^\prime = X^\prime X A.$$Now the gradient $\nabla_b J(b)$ works out to $-2X^\prime e$; substitute $y - XAy$ for $e$ and $\hat{b}$ for $b$, and we have \begin{alignat*}{1} \nabla_{b}J(\hat{b}) & =-2X^{\prime}e\\ & =-2X^{\prime}\left(y-X\hat{b}\right)\\ & =-2X^{\prime}\left(y-XAy\right)\\ & =-2X^{\prime}(I-XA)y\\ & =-2\left(X^{\prime}-X^{\prime}XA\right)y. \end{alignat*}Substitute the aforementioned identity for the middle expression and we have $ \nabla_{b}J(\hat{b}) = 0$. So choosing $b=\hat{b}$ minimizes squared errors and thus gives the proper fitted values.
All that said, I would still rather eliminate redundant predictors. That process can be automated, but if you are writing a machine learning algorithm that will chew through potentially large data sets with no human supervision, and you want to use linear (or polynomial) models, I suppose you should at least consider using the entire data set with the pseudoinverse taking care of the multicollinearity.
Tuesday, October 6, 2015
Producing Reproducible R Code
A tip in the Google+ Statistics and R community led me to the reprex package for R. Quoting the author (Professor Jennifer Bryan, University of British Columbia), the purpose of reprex is to
I'm all for complete and cogent bug reports/code questions and reproducible research, but I was interested in reprex for another reason: formatting R code for blog posts (such as this one). To date I've been using a third party web site (the Pretty R syntax highlighter) to generate HTML from R code, and I've been quite happy with the results. A simpler process would be nice, though. Additional, while the aforementioned site works great with the code, I'm sometimes not sure how I should format the output.
So I decided to take prerex for a test drive using code from an old post here (Tabulating Prediction Intervals in R). I used just the code from the first part of the post (definition of the model.ctable() function and one invocation of it), a total of 17 lines of source code (including Roxygen comments for the function) leading to a single output table. Using RStudio, my work flow was as follows.
That created a border and a bit of padding, and told the browser to add scroll bars if needed. Here is how my example turned out:
You can see the comments, the code and, at the end, the output (formatted as R comments). It's not perfect. In particular, it would be nice if the Roxygen comments looked like comments and not like text. There's also no syntax highlighting (which is to be expected in an R Markdown document). Still, it's not bad for a blog post, and it confirms the package works (and is easy to use).
I'll close by pointing out that I'm going "off label" by using the package this way. In particular, I'm getting no value from one of the prime virtues of R Markdown: the ability to embed code in a text document such that the code can be easily read but can also be executed by "compiling" the document (not true of an HTML document like this post). For posting code to a forum, though, this looks like a definite keeper.
[r]ender reproducible example code to Markdown suitable for use in code-oriented websites, such as StackOverflow.com or GitHub.Much has been written about the virtues of, and need for, reproducible research. Another key need for reproducibility, one at which this package aims, is when posting questions about code or bug reports. Viewers of those posts need to know exactly what you did and exactly what resulted. The readme text on the package's GitHub home page gives a work flow description and some prescriptive advice, which I think is well worth reading.
I'm all for complete and cogent bug reports/code questions and reproducible research, but I was interested in reprex for another reason: formatting R code for blog posts (such as this one). To date I've been using a third party web site (the Pretty R syntax highlighter) to generate HTML from R code, and I've been quite happy with the results. A simpler process would be nice, though. Additional, while the aforementioned site works great with the code, I'm sometimes not sure how I should format the output.
So I decided to take prerex for a test drive using code from an old post here (Tabulating Prediction Intervals in R). I used just the code from the first part of the post (definition of the model.ctable() function and one invocation of it), a total of 17 lines of source code (including Roxygen comments for the function) leading to a single output table. Using RStudio, my work flow was as follows.
- Open a new script file and type/paste the code into it.
- Source the file to confirm it works as expected.
- Copy the code to the clipboard.
- In the console window, run the following two lines.
library(reprex) reprex()
This runs the code in the clipboard, so be careful not to do anything to modify the clipboard contents between the previous step and this one. - Examine the results in the viewer pane (which automatically opens) to confirm that is as expected.
- Open a new R Markdown file, delete the boilerplate RStudio inserts, and paste the contents of the clipboard into it. Along with displaying results in the viewer, the reprex() function also places the R Markdown code for it in the clipboard. Again, be careful not to modify the clipboard contents between step 4 and this one.
- Click the "Knit HTML" button and provide a destination file for the HTML output. This opens an HTML source file in RStudio.
- Copy the contents of the body tag (excluding the opening and closing body tags and ignoring the pile of stuff in the header) and paste into an HTML document. (Depending on the width of the output, you might want to surround it with a scrolling DIV tag, or hack the CSS you just pasted in to make it scrollable and/or give it a border.)
overflow: scroll; border-style: groove; border-width: 5px; padding: 10px;
That created a border and a bit of padding, and told the browser to add scroll bars if needed. Here is how my example turned out:
Summarize a fitted linear model, displaying both coefficient significance and confidence intervals.
@param model an instance of class lm @param level the confidence level (default 0.95)
@return a matrix combining the coefficient summary and confidence intervals
@param model an instance of class lm @param level the confidence level (default 0.95)
@return a matrix combining the coefficient summary and confidence intervals
model.ctable <- function(model, level = 0.95) {
cbind(summary(model)$coefficients, confint(model, level = level))
}
x <- rnorm(20)
y <- rnorm(20)
z <- 6 + 3 * x - 5 * y + rnorm(20)
m <- lm(z ~ x + y)
model.ctable(m, level = 0.9)
#> Estimate Std. Error t value Pr(>|t|) 5 %
#> (Intercept) 6.271961 0.2462757 25.46724 5.584261e-15 5.843539
#> x 2.974000 0.2571237 11.56642 1.763158e-09 2.526706
#> y -4.951286 0.3260552 -15.18542 2.547338e-11 -5.518494
#> 95 %
#> (Intercept) 6.700384
#> x 3.421294
#> y -4.384079You can see the comments, the code and, at the end, the output (formatted as R comments). It's not perfect. In particular, it would be nice if the Roxygen comments looked like comments and not like text. There's also no syntax highlighting (which is to be expected in an R Markdown document). Still, it's not bad for a blog post, and it confirms the package works (and is easy to use).
I'll close by pointing out that I'm going "off label" by using the package this way. In particular, I'm getting no value from one of the prime virtues of R Markdown: the ability to embed code in a text document such that the code can be easily read but can also be executed by "compiling" the document (not true of an HTML document like this post). For posting code to a forum, though, this looks like a definite keeper.
Saturday, September 5, 2015
Another OR Educational Resource
Two years ago (two years and one day if you're being picky), I posted a pointer to a Spanish language web site hosted by Francisco Yuraszeck (professor at the Universidad Técnica Federico Santa María in Viña del Mar, Chile). The site, Gestión de Operaciones, is listed in the resources box on the right. Recently, Francisco informed me that he now has a companion English language site, Linear Programming (LP) and Operations Research (OR) Exercises and Resources for Students. He asked for help getting the word out about it, and I'm happy to do so.
For readers active in the OR community (and in social media), please have a look and, if you like what you see, help publicize the site.
For readers active in the OR community (and in social media), please have a look and, if you like what you see, help publicize the site.
Saturday, August 8, 2015
Optimizing Part of the Objective Function II
Today's post extends yesterday's entry about optimizing a portion of the original objective function. I won't repeat much of the previous post, to save myself some typing.
The actual question motivating these posts, which I originally misread, asked how to minimize, not maximize, the sum of the $K$ largest terms in $\sum_{i=1}^N x_i$ (where $x$ is a vector of decision variables in an optimization model). As I mentioned in the last outing, that (or the symmetric case, maximizing the sum of the $K$ smallest terms), is trickier than what I covered yesterday. Everything from yesterday's post (the introduction of binary variables $z_i$ and auxiliary variables $y_i$ and the added constraints) carries over, with one exception: the objective function is now$$\textrm{minimize} \sum_{i=1}^N y_i.$$On top of all that, we require some additional constraints.
If we do not do something to prevent it, the solver will achieve an ideal objective value of 0 by setting $y_i = 0$ regardless of whether $z_i$ is 0 or 1. So we need additional constraints to ensure that $z_i = 1 \implies y_i = x_i$. We can accomplish that with$$y_i \ge x_i - U_i(1 - z_i)\quad \forall i \in \{1,\dots,N\},$$which forces $y_i\ge x_i$ if $z_i = 1$ and is vacuous if $z_i = 0$.
Choosing the largest of the $x_i$ was automatic when the objective was to maximize the sum. When the objective is minimization, the solver will "want" to choose the smallest of the $x_i$, and we need to constrain it to select the largest values. An easy way to do this is to note that choosing the $K$ largest values is equivalent to saying that every value chosen is at least as big as every value not chosen. Expressed mathematically,$$z_i = 1 \bigwedge z_j = 0 \implies x_i \ge x_j.$$Note that, having assumed $0\le x_k \le U_k\,\forall k$, the most negative that any difference $x_i - x_j$ could be would be $0 - U_j = -U_j$. That leads to the following additional constraints:$$x_i - x_j \ge -U_j(1-z_i+z_j)\quad \forall i,j\in \{1,\dots,N\},\,i\neq j.$$
Coupled with yesterday's formulation, that should get the job done.
The actual question motivating these posts, which I originally misread, asked how to minimize, not maximize, the sum of the $K$ largest terms in $\sum_{i=1}^N x_i$ (where $x$ is a vector of decision variables in an optimization model). As I mentioned in the last outing, that (or the symmetric case, maximizing the sum of the $K$ smallest terms), is trickier than what I covered yesterday. Everything from yesterday's post (the introduction of binary variables $z_i$ and auxiliary variables $y_i$ and the added constraints) carries over, with one exception: the objective function is now$$\textrm{minimize} \sum_{i=1}^N y_i.$$On top of all that, we require some additional constraints.
Update
Forget everything that follows and just skip down to the comments section. There's a clever reformulation, posted by Michael Grant in a comment, that gets the job done with a linear number of new variables (all continuous) and a linear number of constraints. I knew another formulation with no integer variables, and in fact only one new variable at all, but with an exponential number of constraints. I was debating whether to post it until I saw the more efficient solution in Michael's comment.5. Lower bounds on auxiliary variables
If we do not do something to prevent it, the solver will achieve an ideal objective value of 0 by setting $y_i = 0$ regardless of whether $z_i$ is 0 or 1. So we need additional constraints to ensure that $z_i = 1 \implies y_i = x_i$. We can accomplish that with$$y_i \ge x_i - U_i(1 - z_i)\quad \forall i \in \{1,\dots,N\},$$which forces $y_i\ge x_i$ if $z_i = 1$ and is vacuous if $z_i = 0$.
6. Choosing the $K$ largest terms
Choosing the largest of the $x_i$ was automatic when the objective was to maximize the sum. When the objective is minimization, the solver will "want" to choose the smallest of the $x_i$, and we need to constrain it to select the largest values. An easy way to do this is to note that choosing the $K$ largest values is equivalent to saying that every value chosen is at least as big as every value not chosen. Expressed mathematically,$$z_i = 1 \bigwedge z_j = 0 \implies x_i \ge x_j.$$Note that, having assumed $0\le x_k \le U_k\,\forall k$, the most negative that any difference $x_i - x_j$ could be would be $0 - U_j = -U_j$. That leads to the following additional constraints:$$x_i - x_j \ge -U_j(1-z_i+z_j)\quad \forall i,j\in \{1,\dots,N\},\,i\neq j.$$
Coupled with yesterday's formulation, that should get the job done.
Friday, August 7, 2015
Optimizing Part of the Objective Function
A somewhat curious question showed up on a forum today. The author of the question has an optimization model (I'll assume it is either a linear program or mixed integer linear program) of the form
\begin{alignat*}{2}
& \textrm{maximize} & & \sum_{i=1}^{N}x_{i}\\
& \textrm{s.t.} & & x\in\mathcal{X}
\end{alignat*}
where the feasible region $\mathcal{X}$ is presumably polyhedral. What the author wants to do is instead maximize the sum of the $K$ largest terms in the objective, for some fixed $K<N$. The question was how to do this.
In effect, the author wants to selectively turn some terms on and others off in the objective function. Any time I think about turning things on and off, I immediately think of using binary variables as the "switches". That in turn suggests the likely need for auxiliary variables and the very likely need for a priori bounds on the things being turned on and off. Here is one solution, step by step, assuming that the $x$ variables are nonnegative and that we know a finite upper bound $U_i$ for each $x_i$.
So we add variables $z_i \in \{0,1\}$ for $i\in 1\dots N$, with $z_i=1$ if and only if $x_i$ is to be counted.
This is just the constraint $$\sum_{i=1}^N z_i = K$$ (with the option to change the equality to $\le$ if you want up to $K$ terms counted.
We will add real variables $y_1,\dots,y_N$ and make the objective $$\textrm{maximize} \sum_{i=1}^N y_i.$$
Here we benefit from a key property: if we limit the objective function to $K$ terms, the fact that we are maximizing will naturally favor the $K$ largest terms. So we just need the following constraints: \begin{alignat*}{2} y_{i} & \le x_{i} & & \forall i\in\left\{ 1,\dots,N\right\} \\ y_{i} & \le U_{i}z_{i} & \quad & \forall i\in\left\{ 1,\dots,N\right\} . \end{alignat*}If $z_i = 0$, the second constraint will force $y_i=0$ and the term will not contribute to the objective function. If $z_i=1$, the second constraint will become vacuous and the first term will allow $y_i$ to contribute an amount up to $x_i$ to the objective. Since the objective is being maximized, $y_i=x_i$ is certain to occur.
A symmetric version of this will work to minimize the sum of the $K$ smallest terms in the objective.Minimizing the sum of the largest terms or maximizing the sum of the smallest terms is a bit trickier, requiring some extra constraints to enforce $y_i=x_i$ when $z_i = 1$. Oops! It's actually easier, as pointed out in a comment in my next post.
In effect, the author wants to selectively turn some terms on and others off in the objective function. Any time I think about turning things on and off, I immediately think of using binary variables as the "switches". That in turn suggests the likely need for auxiliary variables and the very likely need for a priori bounds on the things being turned on and off. Here is one solution, step by step, assuming that the $x$ variables are nonnegative and that we know a finite upper bound $U_i$ for each $x_i$.
1. Introduce a binary variable for each term to be switched on/off.
So we add variables $z_i \in \{0,1\}$ for $i\in 1\dots N$, with $z_i=1$ if and only if $x_i$ is to be counted.
2. Limit the number of terms to count.
This is just the constraint $$\sum_{i=1}^N z_i = K$$ (with the option to change the equality to $\le$ if you want up to $K$ terms counted.
3. Replace the objective terms with surrogates that can be turned on/off.
We will add real variables $y_1,\dots,y_N$ and make the objective $$\textrm{maximize} \sum_{i=1}^N y_i.$$
4. Connect the surrogate variables to the original variables and the on-off decisions.
Here we benefit from a key property: if we limit the objective function to $K$ terms, the fact that we are maximizing will naturally favor the $K$ largest terms. So we just need the following constraints: \begin{alignat*}{2} y_{i} & \le x_{i} & & \forall i\in\left\{ 1,\dots,N\right\} \\ y_{i} & \le U_{i}z_{i} & \quad & \forall i\in\left\{ 1,\dots,N\right\} . \end{alignat*}If $z_i = 0$, the second constraint will force $y_i=0$ and the term will not contribute to the objective function. If $z_i=1$, the second constraint will become vacuous and the first term will allow $y_i$ to contribute an amount up to $x_i$ to the objective. Since the objective is being maximized, $y_i=x_i$ is certain to occur.
A symmetric version of this will work to minimize the sum of the $K$ smallest terms in the objective.
Sunday, August 2, 2015
More Shiny Hacks
In a previous entry, I posted code for hack I came up with to add vertical scrolling to the sidebar of a web-based application I'm developing in Shiny (using shinydashboard). Since then, I've bumped into two more issues, leading to two more hacks that I'll describe here.
First, I should point out that I'm using the DT 0.1, shiny 0.12.1 and shinydashboard 0.5.0 packages. DT provides an interface to the DataTables JavaScript library, which handles rendering and processing of the table in the browser. Future updates to any of them could make these hacks (and previous one) unnecessary, or could just as easily break them. I also want to emphasize that these are true kludges, not to be held up as examples of good programming practice.
The main body of my application uses tabs, and on one of the tabs I expose a data frame (read only) using DT::dataTableOutput() in the user interface file and DT::renderDataTable() in the server file. The application allows the user to restrict which rows are displayed by setting filters on one or more columns, implemented by adding the option filter = "top" to the invocation of renderDataTable(). Clicking in a filter box expands the box by placing either a double slider (for numeric columns) or a selectize control (for text columns) beneath the box. This will prove to be significant.
In some cases, the data frame will be too wide to fit on one screen. Adding the option scrollX = TRUE to renderDataTable() causes DataTables to add a horizontal scroll bar to the table when needed. According to the documentation for the DT package (the note at the end of section 2.7),
The best solution I could come up with was to omit scrollX = TRUE, which lets the filters behave properly. That leaves the matter of those wide tables to resolve. My solution was to hack the CSS for the user interface. In the earlier post, I showed the CSS hack to get vertical scrolling in the sidebar, adding the following to the .ui file:
To add horizontal scrolling to the data table, when needed, I just add one more line:
So far, that seems to work.
To allow the user to sort the data by one or more columns, I added the following options to renderDataTable():
(The ColVis extension adds a button to let the user select which columns to display, and has nothing to do with the problem at hand.) With the ColReorder extension installed, clicking repeatedly on a column heading toggles between ascending and descending sorts using that column. (Shift-clicking other column headings invokes secondary, tertiary etc. orderings).
That's handy, but what if the user wants to go back to the original ordering? In earlier versions of the DataTables library, clicking a heading cycled through ascending order, descending order and no sort. According to the discussion here, that last option was unintended by the author of DataTables, and he removed it in a recent version. As I read the discussion, it may come back in some future version, but for now it's gone. There are alternative mechanisms to undo the sort, but they currently require a separate control to activate them. As Yihui Xie, the developer of the DT package, points out:
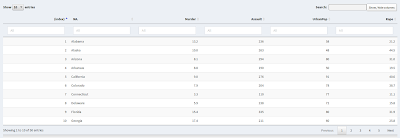
I clicked on the "Murder" column, and then shift-clicked the "NA." (state name) column twice, to sort by ascending murder rate, breaking ties in reverse alphabetical order by state. Note the row numbers on the left and, significantly, the lack of an option to sort on them. In this particular case, the data comes in alphabetical order by state, so sorting on the state column would restore the original order. Other data sets may not come with the data ordered according to any of the variables, so that is not a viable option in general.
My hack is to turn the row indices into a sortable column of data. First, I need to remove the exiting column, which turns out to be the row names of the data frame. In the USArrests data frame, the state names are the row names, but this copy was pulled from a table in an Excel spreadsheet, where the state names were interpreted as a column of data without a column heading (hence the automatically supplied "NA." heading). Since that left the data frame without row names, a default set of names (the row numbers) were automatically supplied.
Removing the row names is easy: add the option rownames = FALSE to the call to renderDataTable(). The next step is to add a column of row indices to the data set. In the server portion of my code, there is a function that lets the user specify an input file and then reads the data into a data frame named x. Adding the line
creates an additional column, with the unconventional (but legal) name "(index)". The column name was chosen in part to make it unlikely that it will collide with an actual column heading. The new column will automatically be given a sort control, as shown in the next screen shot:
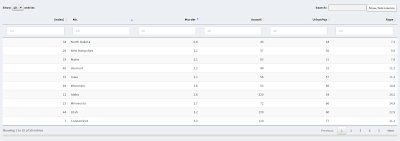
Clicking on the "(index)" column sorts the data into its original order:
Clicking again sorts it into the reverse of the original order, although I do not see that as a particularly useful option.
Note: All syntax highlighting in this post was created by Pretty R at inside-R.org.
First, I should point out that I'm using the DT 0.1, shiny 0.12.1 and shinydashboard 0.5.0 packages. DT provides an interface to the DataTables JavaScript library, which handles rendering and processing of the table in the browser. Future updates to any of them could make these hacks (and previous one) unnecessary, or could just as easily break them. I also want to emphasize that these are true kludges, not to be held up as examples of good programming practice.
The main body of my application uses tabs, and on one of the tabs I expose a data frame (read only) using DT::dataTableOutput() in the user interface file and DT::renderDataTable() in the server file. The application allows the user to restrict which rows are displayed by setting filters on one or more columns, implemented by adding the option filter = "top" to the invocation of renderDataTable(). Clicking in a filter box expands the box by placing either a double slider (for numeric columns) or a selectize control (for text columns) beneath the box. This will prove to be significant.
Problem 1: Horizontal Scrolling
In some cases, the data frame will be too wide to fit on one screen. Adding the option scrollX = TRUE to renderDataTable() causes DataTables to add a horizontal scroll bar to the table when needed. According to the documentation for the DT package (the note at the end of section 2.7),
"The position of column filters may be off when scrolling is enabled in the table, e.g. via the optionsSure enough, if the scrollX option is turned on, the table fails to adjust its vertical spacing properly when the user clicks in a column filter control. As a result, only a very small sliver from the top of the selectize or double slider control is visible, making input nigh unto impossible. This happens whether the filter controls are positioned at the top or bottom of the table.scrollXand/orscrollY."
The best solution I could come up with was to omit scrollX = TRUE, which lets the filters behave properly. That leaves the matter of those wide tables to resolve. My solution was to hack the CSS for the user interface. In the earlier post, I showed the CSS hack to get vertical scrolling in the sidebar, adding the following to the .ui file:
dashboardSidebar( tags$head( tags$style(HTML(" .sidebar { height: 90vh; overflow-y: auto; } " ) ) ), ...
To add horizontal scrolling to the data table, when needed, I just add one more line:
dashboardSidebar( tags$head( tags$style(HTML(" .sidebar { height: 90vh; overflow-y: auto; } .dataTables_wrapper { overflow-x: scroll; } " ) ) ), ...
So far, that seems to work.
Problem 2: Undoing a Row Sort
To allow the user to sort the data by one or more columns, I added the following options to renderDataTable():
(The ColVis extension adds a button to let the user select which columns to display, and has nothing to do with the problem at hand.) With the ColReorder extension installed, clicking repeatedly on a column heading toggles between ascending and descending sorts using that column. (Shift-clicking other column headings invokes secondary, tertiary etc. orderings).
That's handy, but what if the user wants to go back to the original ordering? In earlier versions of the DataTables library, clicking a heading cycled through ascending order, descending order and no sort. According to the discussion here, that last option was unintended by the author of DataTables, and he removed it in a recent version. As I read the discussion, it may come back in some future version, but for now it's gone. There are alternative mechanisms to undo the sort, but they currently require a separate control to activate them. As Yihui Xie, the developer of the DT package, points out:
"It will be awkward to provide a separate button such as Remove Sorting in the UI that does this job."
It may help to start with a screen shot of a typical table, before applying the hack. The data comes from the USArrests data set in the datasets package. |
| Data table before the hack |
I clicked on the "Murder" column, and then shift-clicked the "NA." (state name) column twice, to sort by ascending murder rate, breaking ties in reverse alphabetical order by state. Note the row numbers on the left and, significantly, the lack of an option to sort on them. In this particular case, the data comes in alphabetical order by state, so sorting on the state column would restore the original order. Other data sets may not come with the data ordered according to any of the variables, so that is not a viable option in general.
My hack is to turn the row indices into a sortable column of data. First, I need to remove the exiting column, which turns out to be the row names of the data frame. In the USArrests data frame, the state names are the row names, but this copy was pulled from a table in an Excel spreadsheet, where the state names were interpreted as a column of data without a column heading (hence the automatically supplied "NA." heading). Since that left the data frame without row names, a default set of names (the row numbers) were automatically supplied.
Removing the row names is easy: add the option rownames = FALSE to the call to renderDataTable(). The next step is to add a column of row indices to the data set. In the server portion of my code, there is a function that lets the user specify an input file and then reads the data into a data frame named x. Adding the line
creates an additional column, with the unconventional (but legal) name "(index)". The column name was chosen in part to make it unlikely that it will collide with an actual column heading. The new column will automatically be given a sort control, as shown in the next screen shot:
 |
| Data table (sorted) after hack |
 |
| Data table in original order |
Note: All syntax highlighting in this post was created by Pretty R at inside-R.org.
Tuesday, July 28, 2015
ORiginals - Videos About Research
ORiginals is a YouTube channel co-hosted by Dr. Banafsheh Behzad (@banafsheh_b) of CSU Long Beach and my colleague Dr. David Morrison (@drmorr0). They present short (five or six minute) videos featuring researchers describing their research to a general (non-expert) audience. Their tag line is "Outstanding research in everyday language", and I think the first two installments have lived up to that mantra.
The first two videos, by Dr. Behzad and the net-biquitous Dr. Laura McLay (@lauramclay) of the University of Wisconsin, fall into the category of operations research. The aim of the channel, however, is more general. Quoting Dr. Behzad:
 )
)
The first two videos, by Dr. Behzad and the net-biquitous Dr. Laura McLay (@lauramclay) of the University of Wisconsin, fall into the category of operations research. The aim of the channel, however, is more general. Quoting Dr. Behzad:
The goal of ORiginals is to promote science and engineering topics among the general public, using everyday language. We are featuring a diverse selection of scientists doing cutting-edge research. This is the first season of ORiginals and even though we aren't specifically OR/MS-focused, we'll have a slight bias in that direction with our guest selection, as David and I are both OR people.If you're interested in seeing quality research explained in lay terms, I highly recommend subscribing to the channel. If you're doing scientific/engineering research that has measurable impact (or the potential for measurable impact) in the real world (sorry, boson-chasers), and you'd like to spread the gospel, I suggest you contact one of the co-hosts. (They're millennials, so a DM on Twitter is probably more effective than an email message.
Saturday, July 25, 2015
Shiny Hack: Vertical Scrollbar
I bumped into a scrolling issue while writing a web-based application in Shiny, using the shinydashboard package. Actually, there were two separate problems.
As a kludge to get around the first problem, which in my app is triggered by extensive help text (and some input controls) in the sidebar that makes the sidebar taller than the main body, I decided to introduce a separate vertical scrollbar in the sidebar. That turned out to be tricky, or at least I could not find an easy, documented method. I thought I would share the code that ultimately did the job for me. I goes in the ui.R file.
Created by Pretty R at inside-R.org
The height: 90vh style attribute sets the height of the sidebar at 90% of the viewport height, so that it adjusts automatically if the user maximizes or resizes the window, opens or closes a tool bar, etc. You need to pick a percentage that works for your particular application. Make it too large and the inability to scroll to the bottom of the sidebar will persist. Make it too small and the sidebar will be noticeably shorter than the main body, leaving a gap at the bottom of the sidebar (and introducing a vertical scrollbar when the entire sidebar is already visible).
Three last notes on the scrolling issue:
- The browser apparently cannot discern page height. In Firefox and Chrome, this resulted in vertical scrollbars that could scroll well beyond the bottom of a page. That's mildly odd, but not a problem as far as I'm concerned. In Internet Exploder, however, the page height was underestimated, and as a result in some cases it was not possible to reach the bottom of the page (at least not with the vertical scrollbar).
- In Internet Exploder only, the viewport scrollbar, on the right side of the window, behaves intermittently. If I click on the "elevator car" (handle) while it is at the top of the bar, it jumps to the bottom of the track, and the spot where I clicked gains a duplicate copy of the up arrow icon that appears just above the handle. If the handle is at the bottom of the bar, it behaves symmetrically. The down arrow icon on the vertical scrollbar lets you scroll downward, but not fully to the bottom of the page.
As a kludge to get around the first problem, which in my app is triggered by extensive help text (and some input controls) in the sidebar that makes the sidebar taller than the main body, I decided to introduce a separate vertical scrollbar in the sidebar. That turned out to be tricky, or at least I could not find an easy, documented method. I thought I would share the code that ultimately did the job for me. I goes in the ui.R file.
dashboardSidebar( tags$head( tags$style(HTML(" .sidebar { height: 90vh; overflow-y: auto; } " ) ) ), ...
The height: 90vh style attribute sets the height of the sidebar at 90% of the viewport height, so that it adjusts automatically if the user maximizes or resizes the window, opens or closes a tool bar, etc. You need to pick a percentage that works for your particular application. Make it too large and the inability to scroll to the bottom of the sidebar will persist. Make it too small and the sidebar will be noticeably shorter than the main body, leaving a gap at the bottom of the sidebar (and introducing a vertical scrollbar when the entire sidebar is already visible).
Three last notes on the scrolling issue:
- In my application, the scrolling problem only appeared on pages where the sidebar was taller than the main body (as far as I know).
- Although the vertical scrollbar in IE is balky, scrolling via the mouse wheel (if you have one) or the arrow keys seems to work fine.
- This is as yet untested on Safari.
Thursday, July 23, 2015
Autocorrupt in R
You know that "autocomplete" feature on your smart phone or tablet that occasionally (or, in my case, frequently) turns into an "autocorrupt" feature? I just ran into it in an R script.
I wrote a web-based application for a colleague that lets students upload data, run a regression, ponder various outputs and, if they wish, export (download) selected results. In the server script, I created an empty list named "export". As users generated various outputs, they would be added to the list for possible download (to avoid having to regenerate them at download time). For instance, if the user generated a histogram of the residuals, then the plot would be stored in export$hist. Similarly, if the user looked at the adjusted R-squared, it would be parked in export$adjr2.
All was well until, in beta testing, I bumped into a bug involving the p-value for the F test of overall fit (you know, the test where failure to reject the null hypothesis would signal that your model contended for the worst regression model in the history of statistics). Rather than getting a single number between 0 and 1, in one test it printed out as a vector of numbers well outside that range. Huh???
I beat my head against an assortment of flat surfaces before I found the bug. The following chunk of demonstration code sums it up.
Created by Pretty R at inside-R.org
The intent was to store the p-value of the test of overall fit in export$f, and the fitted values in export$fitted. If the user never checked the F test, I wanted export$f to be null, which would signal the export subroutine to skip it. Instead, the export subroutine autocompleted export$f (which did not exist) to export$fitted (which did exist) and spat out the mystery vector. There are multiple ways to avoid the bug, the simplest being to rename export$f to something like export$fprob, where "fprob" is not a substring of the name of any other entry of export.
I do my R coding inside RStudio, which provides autocompletion suggestions. Somewhere along the line, I think I came across the fact that the R interpreter autocompletes some things. It never occurred to me that this would happen when a script ran. When running commands interactively, I suppose the autocomplete feature saves some keystrokes. That's not generally an issue when running scripts, so I don't know why autocomplete is not turned off when "sourcing" a script.
At any rate, letting the betting commence on how long it will take me to forget this (and trip over it again).
I wrote a web-based application for a colleague that lets students upload data, run a regression, ponder various outputs and, if they wish, export (download) selected results. In the server script, I created an empty list named "export". As users generated various outputs, they would be added to the list for possible download (to avoid having to regenerate them at download time). For instance, if the user generated a histogram of the residuals, then the plot would be stored in export$hist. Similarly, if the user looked at the adjusted R-squared, it would be parked in export$adjr2.
All was well until, in beta testing, I bumped into a bug involving the p-value for the F test of overall fit (you know, the test where failure to reject the null hypothesis would signal that your model contended for the worst regression model in the history of statistics). Rather than getting a single number between 0 and 1, in one test it printed out as a vector of numbers well outside that range. Huh???
I beat my head against an assortment of flat surfaces before I found the bug. The following chunk of demonstration code sums it up.
The intent was to store the p-value of the test of overall fit in export$f, and the fitted values in export$fitted. If the user never checked the F test, I wanted export$f to be null, which would signal the export subroutine to skip it. Instead, the export subroutine autocompleted export$f (which did not exist) to export$fitted (which did exist) and spat out the mystery vector. There are multiple ways to avoid the bug, the simplest being to rename export$f to something like export$fprob, where "fprob" is not a substring of the name of any other entry of export.
I do my R coding inside RStudio, which provides autocompletion suggestions. Somewhere along the line, I think I came across the fact that the R interpreter autocompletes some things. It never occurred to me that this would happen when a script ran. When running commands interactively, I suppose the autocomplete feature saves some keystrokes. That's not generally an issue when running scripts, so I don't know why autocomplete is not turned off when "sourcing" a script.
At any rate, letting the betting commence on how long it will take me to forget this (and trip over it again).
Thursday, July 2, 2015
Tabulating Prediction Intervals in R
I just wrapped up (knock on wood!) a coding project using R and Shiny. (Shiny, while way cool, is incidental to this post.) It was a favor for a friend, something she intends to use teaching an online course. Two of the tasks, while fairly mundane, generated code that was just barely obscure enough to be possibly worth sharing. It's straight R code, so you need not use (or have installed) Shiny to use it.
The first task was to output, in tabular form, the coefficients of a linear regression model, along with their respective confidence intervals. The second task was to output, again in tabular form, the fitted values, confidence intervals and prediction intervals for the same model. Here is the function I wrote to do the first task (with Roxygen comments):
To demonstrate its operation, I'll generate a small sample with random data and run a linear regression on it.
I'll generate the coefficient table using confidence level 0.9, rather than the default 0.95, for the coefficients.
The output is as follows:
The code for the second table (fits, confidence intervals and prediction intervals) is a bit longer:
Here is the call with default arguments (using head() to limit the amount of output):
The output is this:
The output is:
The first task was to output, in tabular form, the coefficients of a linear regression model, along with their respective confidence intervals. The second task was to output, again in tabular form, the fitted values, confidence intervals and prediction intervals for the same model. Here is the function I wrote to do the first task (with Roxygen comments):
#' #' Summarize a fitted linear model, displaying both coefficient significance #' and confidence intervals. #' #' @param model an instance of class lm #' @param level the confidence level (default 0.95) #' #' @return a matrix combining the coefficient summary and confidence intervals #' model.ctable <- function(model, level = 0.95) { cbind(summary(model)$coefficients, confint(model, level = level)) }
To demonstrate its operation, I'll generate a small sample with random data and run a linear regression on it.
I'll generate the coefficient table using confidence level 0.9, rather than the default 0.95, for the coefficients.
model.ctable(m, level = 0.9)
Estimate Std. Error t value Pr(>|t|) 5 % 95 % (Intercept) 6.039951 0.2285568 26.42648 3.022477e-15 5.642352 6.437550 x 3.615331 0.2532292 14.27691 6.763279e-11 3.174812 4.055850 y -5.442428 0.3072587 -17.71285 2.156161e-12 -5.976937 -4.907918
The code for the second table (fits, confidence intervals and prediction intervals) is a bit longer:
#' #' Compute a table of fitted values, confidence intervals and #' prediction intervals from a regression model. #' #' @param model a fitted regression model #' @param level the desired confidence level (default 0.95) #' @param names the names to assign to the columns (after #' resequencing if necessry) #' @param order the order in which to list the columns #' (1 = fitted, 2 = lower c.i. limit, 3 = upper c.i. limit, #' 4 = lower p.i. limit, 5 = upper p.i. limit) #' #' @return a matrix with one row per observation and five #' columns (fitted value, lower/upper c.i. bounds, lower/upper #' p.i. bounds) in the order specified by the user #' intervals <- function(model, level = 0.95, names = c("Fitted", "CI Low", "CI High", "PI Low", "PI High"), order = c(4, 2, 1, 3, 5)) { # generate fits and confidence intervals temp <- predict(model, interval = "confidence", level = level) # generate fits and prediciton intervals (suppressing # the warning about predicting past values) temp2 <- suppressWarnings( predict(model, interval = "prediction", level = level) ) # drop the redundant fit column temp2 <- temp2[,2:3] # merge the tables and reorder the columns temp <- cbind(temp, temp2)[, order] # rename the columns colnames(temp) <- names[order] temp }
Here is the call with default arguments (using head() to limit the amount of output):
The output is this:
PI Low CI Low Fitted CI High PI High 1 -0.7928115 0.65769280 1.5196870 2.381681 3.832185 2 7.9056270 9.40123642 10.1928094 10.984382 12.479992 3 4.9125024 6.61897662 7.1149000 7.610823 9.317298 4 7.3386447 8.66123993 9.7406923 10.820145 12.142740 5 -1.4295587 0.05464529 0.8637503 1.672855 3.157059 6 4.1962493 5.84893725 6.4156619 6.982387 8.635074Finally, I'll run it again, changing the confidence level to 0.9, tweaking the column headings a bit, and reordering them:
The output is:
Fit CI_l CI_u PI_l PI_u
1 1.5196870 0.8089467 2.230427 -0.3870379 3.426412
2 10.1928094 9.5401335 10.845485 8.3069584 12.078660
3 7.1149000 6.7059962 7.523804 5.2989566 8.930843
4 9.7406923 8.8506512 10.630733 7.7601314 11.721253
5 0.8637503 0.1966188 1.530882 -1.0271523 2.754653
6 6.4156619 5.9483803 6.882943 4.5856891 8.245635
By the way, all syntax highlighting was Created by Pretty R at inside-R.org.
Saturday, June 27, 2015
The rJava Nightmare
I like R. I like Java. I hate the rJava package, or more precisely I hate installing or updating it. Something (often multiple somethings) always goes wrong. I forget that for some reason I need to invoke root privileges when installing it. It needs a C++ library that I could swear I have, except I don't have the developer version of that library installed. Whatever. See this post from 2011 for a previous misadventure.
Today's battle was fought after a "successful" installation on my laptop. The good news: the package was installed, and RStudio knew it was installed. The bad news: neither RStudio, nor R run in a terminal, would let me load it. The key nugget in the error message:
Fortunately, my laptop and desktop both run the same OS (Linux Mint), pretty much the same version, and rJava was working fine on the desktop. So the trick was to figure out how they differed. The route to libjvm.so does not appear in LD_LIBRARY_PATH on my PC, and is not mentioned in either of those profile files. It turns out that the path is set in the profile for R (/usr/lib/R/etc/ldpaths, to be specific), in the definition of a new variable R_JAVA_LD_LIBRARY_PATH. On the laptop, that was set to ${JAVA_HOME}/lib/amd64/server; on the PC, it was ${JAVA_HOME}/jre/lib/amd64/server. The latter path is correct on both the PC and the laptop. So I edited ldpaths on the laptop (as root), inserted the missing piece of the path, and lo and behold both R in a terminal and R inside RStudio could execute "library(rJava)" without bellyaching!
Note that, per my 2011 post, I had run sudo R CMD javareconf (more than once), with the correct value of the JAVA_HOME environment variable in place. Why that did not fix the path in ldpaths, and why the path was wrong in the first place, remain mysteries to me.
Update (12/30/16): I ran into the same problem, with a somewhat different cause. Updated details are in this post.
Today's battle was fought after a "successful" installation on my laptop. The good news: the package was installed, and RStudio knew it was installed. The bad news: neither RStudio, nor R run in a terminal, would let me load it. The key nugget in the error message:
Now libjvm.so was definitely installed (as part of Oracle Java 8), so this was a matter of somehow breaking the news to R and/or RStudio. Search for "rJava" and "libjvm" on Google and you'll find a lot of hits, because I'm apparently not the first person to trip over this. Most solutions involving adding the requisite directory (which for me is ${JAVA_HOME}/jre/lib/amd64/server) to the LD_LIBRARY_PATH environment variable in your .profile file. I tried both that and .bashrc, with the result that R in a terminal agreed to load rJava but R running in RStudio still did not. Some of the posts I found said that this was expected if you made the tweeked .bashrc, but tweaking .profile instead was supposed to fix things. Except it didn't.libjvm.so: cannot open shared object file: No such fileordirectory
Fortunately, my laptop and desktop both run the same OS (Linux Mint), pretty much the same version, and rJava was working fine on the desktop. So the trick was to figure out how they differed. The route to libjvm.so does not appear in LD_LIBRARY_PATH on my PC, and is not mentioned in either of those profile files. It turns out that the path is set in the profile for R (/usr/lib/R/etc/ldpaths, to be specific), in the definition of a new variable R_JAVA_LD_LIBRARY_PATH. On the laptop, that was set to ${JAVA_HOME}/lib/amd64/server; on the PC, it was ${JAVA_HOME}/jre/lib/amd64/server. The latter path is correct on both the PC and the laptop. So I edited ldpaths on the laptop (as root), inserted the missing piece of the path, and lo and behold both R in a terminal and R inside RStudio could execute "library(rJava)" without bellyaching!
Note that, per my 2011 post, I had run sudo R CMD javareconf (more than once), with the correct value of the JAVA_HOME environment variable in place. Why that did not fix the path in ldpaths, and why the path was wrong in the first place, remain mysteries to me.
Update (12/30/16): I ran into the same problem, with a somewhat different cause. Updated details are in this post.
Thursday, June 25, 2015
Selecting the Least Qualifying Index
Something along the following lines cropped up recently, regarding a discrete optimization model. Suppose that we have a collection of binary variables $x_i \in B, \, i \in 1,\dots,N$ in an optimization model, where $B=\{0, 1\}$. The values of the $x_i$ will of course be dictated by the combination of the constraints and objective function. Now suppose further that we want to identify the smallest index $i$ for which $x_i = 1$ for use within the model (hence before solving the model). I'll consider two possibilities:
To handle the second case, we can add the following constraints: \begin{alignat*}{2}
y_{i} & \le x_{i} & \; & \forall i\\
y_{i} & \ge x_{i}-\sum_{j<i}x_{j} & & \forall i\\
iy_{i} & \le i-\sum_{j<i}x_{j} & & \forall i>1
\end{alignat*}Left to the reader as an exercise: to confirm that this works (or, if you find an error, to kindly post it in a comment).
- we want to store that minimal index in an integer variable (which I will call $z$); or
- we want to create an alternative set of binary variables ($y_i \in B, \, i \in 1,\dots,N$) where \[ y_{i}=1\iff i=\text{argmin}\left\{ j:x_{j}=1\right\}. \]
To handle the second case, we can add the following constraints: \begin{alignat*}{2}
y_{i} & \le x_{i} & \; & \forall i\\
y_{i} & \ge x_{i}-\sum_{j<i}x_{j} & & \forall i\\
iy_{i} & \le i-\sum_{j<i}x_{j} & & \forall i>1
\end{alignat*}Left to the reader as an exercise: to confirm that this works (or, if you find an error, to kindly post it in a comment).
Friday, June 19, 2015
Alternative Versions of R
Fair warning: most of this post is specific to Linux users, and in fact to users of Debian-based distributions (e.g., Debian, Ubuntu or Mint). The first section, however, may be of interest to R users on any platform.
Revolution Analytics is now a Microsoft property, and I can't being to describe the cognitive dissonance caused by downloading open-source software from Microsoft. Nonetheless, I decided to install RROpen. One catch is that it requires reinstalling pretty much every R package I use, which can be a bit time consuming. The remainder of this post is about the other catch: how to get RROpen and "official" R (henceforth "R" without any qualifications) to coexist peacefully, on a Debian-based distribution (Mint in my case).
That can be fixed manually from a terminal (as root), but it appeared that I was doomed to perpetually mediating between the two versions whenever the r-base package updated. This could be why Rich Gillin ("owner" of the Google+ Statistics and R community) recommended uninstalling R before installing RRO.
Debian-based distributions of Linux use the Debian alternatives system to manage contention between different programs that have the same use. In essence, the system puts a link in a directory on the system command path that points not to a specific executable but to a directory containing choices for what program should answer to that name. Applied to our case, /usr/bin/R becomes a symbolic link to /etc/alternatives/R, which in turn is a symbolic link to the version of R you want to execute when you type R at a command prompt (or when, say, the RStudio IDE launches). In my case, that link points to /usr/lib64/RRO-3.2.0/R-3.2.0/lib/R/bin/R. (How would like to have to type that every time you wanted to run RRO?)
To manage alternatives, you can either use the update-alternatives command in a terminal or the Galternatives GUI for it. On my system, though, Galternatives does not entirely work. It lets you add alternatives once a base configuration is set, but it will not let you create (or delete) the initial configuration. So I went with the command line.
Assuming you have both RRO and R installed, here are the commands to set them up as alternatives:
The anatomy of the middle line is as follows:
The first time I tried this (with /usr/bin/R being the RRO executable), I omitted the first line, and update-alternatives informed me that it had not created /usr/bin/R (presumably because it was reluctant to overwrite what was already there, despite running with root privileges). So I suggest deleting the current entry before setting up the alternatives. Also, as an aside, after running the first two lines, I was able to us Galternatives to enter the third one, and I can use Galternatives to change which is the default choice for R.
I tried reinstalling the r-base package after doing this, and the default R choice remained RRO, so I think this will survive upgrades to either system. We'll see.
An alternative to "official" R
By "official" R, I mean the version of R issued by the R Foundation. Revolution Analytics has been a source of information, courses and a beefed-up commercial version of R (Revolution R Enterprise). They have also produced an open-source version, Revolution R Open. It is freely available from their Managed R Archive Network (MRAN). I'll leave the description of its features to them, and just mention the one that caught my eye: coupled with the Intel Math Kernel Library, it provides out-of-the-box multithreading, which should speed up long computational runs.Revolution Analytics is now a Microsoft property, and I can't being to describe the cognitive dissonance caused by downloading open-source software from Microsoft. Nonetheless, I decided to install RROpen. One catch is that it requires reinstalling pretty much every R package I use, which can be a bit time consuming. The remainder of this post is about the other catch: how to get RROpen and "official" R (henceforth "R" without any qualifications) to coexist peacefully, on a Debian-based distribution (Mint in my case).
What's the problem?
RRO and R install in different directories, so why is anything special necessary to let them coexist? I found out the hard way. After installing RRO (on a system that already had R), I found that the command R in a terminal launched /usr/bin/R, which RRO had replaced with its R binary, making itself the default choice. That was fine for me. This morning, though, the system package manager notified me that the r-base package had been updated. I authorized the update, which among other things resulted in <sigh>/usr/bin/R being replaced by the "official" R version</sigh>.That can be fixed manually from a terminal (as root), but it appeared that I was doomed to perpetually mediating between the two versions whenever the r-base package updated. This could be why Rich Gillin ("owner" of the Google+ Statistics and R community) recommended uninstalling R before installing RRO.
What's the solution?
Debian-based distributions of Linux use the Debian alternatives system to manage contention between different programs that have the same use. In essence, the system puts a link in a directory on the system command path that points not to a specific executable but to a directory containing choices for what program should answer to that name. Applied to our case, /usr/bin/R becomes a symbolic link to /etc/alternatives/R, which in turn is a symbolic link to the version of R you want to execute when you type R at a command prompt (or when, say, the RStudio IDE launches). In my case, that link points to /usr/lib64/RRO-3.2.0/R-3.2.0/lib/R/bin/R. (How would like to have to type that every time you wanted to run RRO?)
To manage alternatives, you can either use the update-alternatives command in a terminal or the Galternatives GUI for it. On my system, though, Galternatives does not entirely work. It lets you add alternatives once a base configuration is set, but it will not let you create (or delete) the initial configuration. So I went with the command line.
Assuming you have both RRO and R installed, here are the commands to set them up as alternatives:
sudo rm /usr/bin/R sudo update-alternatives --install /usr/bin/R R /usr/lib64/RRO-3.2.0/R-3.2.0/lib/R/bin/R 200 sudo update-alternatives --install /usr/bin/R R /usr/lib/R/bin/R 100
The anatomy of the middle line is as follows:
- sudo
- Run this stuff as root.
- update-alternatives
- Run the configuration update tool.
- --install
- I want to install a new alternative for a program. Other choices include --configure to alter the default choice, --list to show alternatives for a program, and --display to show a list including priorities.
- /usr/bin/R
- Where the link to the various alternatives will go. This should be somewhere on your command path. A program (such as RStudio) trying to execute R with no path, or using the default path for R, will look here and be forwarded to the chosen version. Similarly, if you just type R in a terminal, this is the program that will run.
- R
- The name used in the alternatives directory for the symbolic link to the actual executable.
- /usr/lib64/RRO-3.2.0/R-3.2.0/lib/R/bin/R
- The executable to be run.
- 200
- A priority value. The highest priority alternative becomes the default choice, unless you manually override it.
The first time I tried this (with /usr/bin/R being the RRO executable), I omitted the first line, and update-alternatives informed me that it had not created /usr/bin/R (presumably because it was reluctant to overwrite what was already there, despite running with root privileges). So I suggest deleting the current entry before setting up the alternatives. Also, as an aside, after running the first two lines, I was able to us Galternatives to enter the third one, and I can use Galternatives to change which is the default choice for R.
I tried reinstalling the r-base package after doing this, and the default R choice remained RRO, so I think this will survive upgrades to either system. We'll see.
Saturday, May 30, 2015
Decision Analytics and Teacher Qualifications
Disclaimers:
The genesis of today's post is a blog entry I read on Spartan Ideas titled "Is Michigan Turning Away Good Teachers?" (Spartan Ideas is a "metablog", curated by our library, that reposts other blogs by members of the Michigan State University community. The original post can be found here.) The focus of that post is on changes to the certification examination that would-be teachers in Michigan are required to pass. I'll quote a couple of key passages here, but invite you to read the full post to get the entire context:
My first reaction to the "weak" connection between teacher characteristics and learning outcomes is that it sounded like bad news for people on all sides of the current debates about educational reform. On the one hand, to the "blame the teacher" crowd (who like to attribute perceived problems in the public education system to poor or bad teachers, teacher tenure etc.), one might say that if teacher quality explains "only" 8% of variance in learning outcomes, quit picking on them and look elsewhere. On the other hand, to people (often affiliated with teacher unions) pushing for better compensation, better working conditions etc., one might point out that those are generally incentives to recruit and retain better teachers; so if teacher quality explains "only" 8% of variance in learning outcomes, perhaps those dollars are better spent elsewhere (upgrading schools, improving neighborhood economic conditions, ...).
What struck me second about the original post was the use of the phrases "only about" and "weak predictors". This seems to me to relate to a difference between statistics, as it is commonly taught (and used), and what some people now refer to as "decision analytics". In my experience, the primary focus of statistics (and its sibling "data analytics") is to identify patterns and explain things (along with making predictions). That makes measures such as correlation and percentage of dependent variance explained relevant. In contrast, decision analytics emphasizes changing things. Where are we now, where do we want to be, which levers can we pull to help us get there, how much should we pull each, and what will it cost us to do so? That perspective may put more emphasis on measures of location (such as means), and on which input factors provide us "leverage" (in the archimedean sense of the term, not the regression sense), than on measures of dispersion (variance).
It is common, at least in the social sciences, to categorize predictors as "strong" or "weak" according to how much variation in the dependent variable they predict. This is the statistics perspective. I understand the attractiveness of this, particularly when the point of the model is to "explain" what happens in the dependent variable. At the same time, I think this categorization can be a bit dangerous from a decision analytics standpoint.
Fair warning: I'm about to start oversimplifying things, for the sake of clarity (and to reduce how much typing I need to do). Suppose that I have a unidimensional measure $L$ of learning outcomes and a unidimensional measure $T$ of teacher quality. Suppose further that I posit a linear model (since I'm all about simplicity today) of the form $$L = \alpha + \beta T + \epsilon$$with $\epsilon$ the "random noise" component (the aggregation of all things not related to teacher quality). Let's assume that $T$ and $\epsilon$ are independent of each other, which gives me the usual (for regression) decomposition of variances:$$\sigma_L^2 = \beta^2 \sigma_T^2 + \sigma_\epsilon^2.$$From the research cited above, we expect to find $\beta^2 \sigma_T^2$ to be about 8% of $\sigma_L^2$.
Tell a decision analyst that the goal is to "improve learning", and something all the lines of the following questions should arise:
In my simplified version of the regression model, $\Delta L = \beta \Delta T$. The same ingredients that lead to the estimate of 8% variance explained also allow us to take an educated guess whether $\beta$ is really zero (teacher quality does not impact learning; what we're seeing in the data is a random effect) and to estimate a confidence interval $[\beta_L, \beta_U]$ for $\beta$. Assuming that $\beta_L > 0$, so that we are somewhat confident teacher quality relates positively to learning outcomes, and assuming for convenience that our goals are expressed in terms of mean learning outcome, a decision analyst should focus on identifying ways to increase $T$ (and, in the process, a plausible range of attainable values for $\Delta T$), the benefit of the outcome $\Delta L$ for any attainable $\Delta T$, and the cost of that $\Delta T$.
Stricter teacher certification exams may be a way to increase teacher quality. Assuming that certification requirements do in fact improve teacher quality (which is a separate statistical assessment), and assuming that we do not want to increase class sizes or turn students away (and therefore need to maintain approximately the same size teaching work force), imposing tighter certification standards will likely result in indirect costs (increasing salaries or benefits to attract and retain the better teachers, creating recruiting programs to draw more qualified people into the profession, ...). As with the connection between teacher quality and learning outcomes, the connecting between certification standards and teacher quality may be weak in the statistical sense (small amount of variance explained), but our hypothetical analyst still needs to assess the costs and impacts to see if it is a cost-effective lever to pull.
So, to recap the point I started out intending to make (which may have gotten lost in the above), explaining variance is a useful statistical concept but decision analysis should be more about cost-effective ways to move the mean/median/whatever.
And now I feel that I should take a pledge to avoid the word "assuming" for at least a week ... assuming I can remember to keep the pledge.
- This a post about statistics versus decision analytics, not a prescription for improving the educational system in the United States (or anywhere else, for that matter).
- tl;dr.
The genesis of today's post is a blog entry I read on Spartan Ideas titled "Is Michigan Turning Away Good Teachers?" (Spartan Ideas is a "metablog", curated by our library, that reposts other blogs by members of the Michigan State University community. The original post can be found here.) The focus of that post is on changes to the certification examination that would-be teachers in Michigan are required to pass. I'll quote a couple of key passages here, but invite you to read the full post to get the entire context:
Research has found that only about 8% of the differences in student achievement can be attributed to teachers and only 3% of that can be attributed to the combined impact of teachers’ certification, ACT/SAT scores, degrees, and experience.
...
Because teachers’ examination scores have been found to be only weak predictors of their impact on student learning, an assessment that has a low pass rate by design may prevent some who would be effective teachers from obtaining a teaching certificate, a concern that is supported by research.(The link in the quote is a 2002 article in Education Next by Dan Goldhaber, senior research associate at the Urban Institute.)
My first reaction to the "weak" connection between teacher characteristics and learning outcomes is that it sounded like bad news for people on all sides of the current debates about educational reform. On the one hand, to the "blame the teacher" crowd (who like to attribute perceived problems in the public education system to poor or bad teachers, teacher tenure etc.), one might say that if teacher quality explains "only" 8% of variance in learning outcomes, quit picking on them and look elsewhere. On the other hand, to people (often affiliated with teacher unions) pushing for better compensation, better working conditions etc., one might point out that those are generally incentives to recruit and retain better teachers; so if teacher quality explains "only" 8% of variance in learning outcomes, perhaps those dollars are better spent elsewhere (upgrading schools, improving neighborhood economic conditions, ...).
What struck me second about the original post was the use of the phrases "only about" and "weak predictors". This seems to me to relate to a difference between statistics, as it is commonly taught (and used), and what some people now refer to as "decision analytics". In my experience, the primary focus of statistics (and its sibling "data analytics") is to identify patterns and explain things (along with making predictions). That makes measures such as correlation and percentage of dependent variance explained relevant. In contrast, decision analytics emphasizes changing things. Where are we now, where do we want to be, which levers can we pull to help us get there, how much should we pull each, and what will it cost us to do so? That perspective may put more emphasis on measures of location (such as means), and on which input factors provide us "leverage" (in the archimedean sense of the term, not the regression sense), than on measures of dispersion (variance).
It is common, at least in the social sciences, to categorize predictors as "strong" or "weak" according to how much variation in the dependent variable they predict. This is the statistics perspective. I understand the attractiveness of this, particularly when the point of the model is to "explain" what happens in the dependent variable. At the same time, I think this categorization can be a bit dangerous from a decision analytics standpoint.
Fair warning: I'm about to start oversimplifying things, for the sake of clarity (and to reduce how much typing I need to do). Suppose that I have a unidimensional measure $L$ of learning outcomes and a unidimensional measure $T$ of teacher quality. Suppose further that I posit a linear model (since I'm all about simplicity today) of the form $$L = \alpha + \beta T + \epsilon$$with $\epsilon$ the "random noise" component (the aggregation of all things not related to teacher quality). Let's assume that $T$ and $\epsilon$ are independent of each other, which gives me the usual (for regression) decomposition of variances:$$\sigma_L^2 = \beta^2 \sigma_T^2 + \sigma_\epsilon^2.$$From the research cited above, we expect to find $\beta^2 \sigma_T^2$ to be about 8% of $\sigma_L^2$.
Tell a decision analyst that the goal is to "improve learning", and something all the lines of the following questions should arise:
- How do we measure "learning"? (Assume that's our $L$ here.)
- What is our goal (achieve the biggest bang on a fixed budget, achieve a fixed target at minimal cost, ...)?
- Is the goal expressed in terms of mean result, median result, achievement by students at some fractile of the learning distribution (e.g., boost the bottom quartile of $L$ to some level), or something else (e.g., beat those pesky Taiwanese kids on international math tests)? Reducing variance in $L$, or the range of $L$, could be a goal, but I doubt it would be many people's first choice, since a uniform level of mediocrity would achieve it.
- What are our levers? Teacher quality (our $T$) would seem to be one. Improving other measures of school quality (infrastructure, information technology) might be another. We might also look at improving socioeconomic factors, either at the school (more free lunches or even breakfasts, more after-school activities, more security on the routes to and from the schools) or elsewhere (safer neighborhoods, better food security, more/better jobs, programs to support two-parent households, ...).
- How much progress toward our goal do we get from feasible changes to each of those levers?
- What does it cost us to move those levers?
In my simplified version of the regression model, $\Delta L = \beta \Delta T$. The same ingredients that lead to the estimate of 8% variance explained also allow us to take an educated guess whether $\beta$ is really zero (teacher quality does not impact learning; what we're seeing in the data is a random effect) and to estimate a confidence interval $[\beta_L, \beta_U]$ for $\beta$. Assuming that $\beta_L > 0$, so that we are somewhat confident teacher quality relates positively to learning outcomes, and assuming for convenience that our goals are expressed in terms of mean learning outcome, a decision analyst should focus on identifying ways to increase $T$ (and, in the process, a plausible range of attainable values for $\Delta T$), the benefit of the outcome $\Delta L$ for any attainable $\Delta T$, and the cost of that $\Delta T$.
Stricter teacher certification exams may be a way to increase teacher quality. Assuming that certification requirements do in fact improve teacher quality (which is a separate statistical assessment), and assuming that we do not want to increase class sizes or turn students away (and therefore need to maintain approximately the same size teaching work force), imposing tighter certification standards will likely result in indirect costs (increasing salaries or benefits to attract and retain the better teachers, creating recruiting programs to draw more qualified people into the profession, ...). As with the connection between teacher quality and learning outcomes, the connecting between certification standards and teacher quality may be weak in the statistical sense (small amount of variance explained), but our hypothetical analyst still needs to assess the costs and impacts to see if it is a cost-effective lever to pull.
So, to recap the point I started out intending to make (which may have gotten lost in the above), explaining variance is a useful statistical concept but decision analysis should be more about cost-effective ways to move the mean/median/whatever.
And now I feel that I should take a pledge to avoid the word "assuming" for at least a week ... assuming I can remember to keep the pledge.
Sunday, May 17, 2015
Feelings of Rejection
This is a quick (?) recap of an answer I posted on a support forum earlier today. I will couch it in terms somewhat specific to CPLEX, but with minor tweaks it should apply to other mixed-integer programming solvers as well.
It is possible to "warm start" CPLEX (and, I'm pretty sure, at least some other solvers) by feeding it an initial solution, or a partial solution (meaning values for some but not all variables). CPLEX will try to complete the solution if necessary, test for feasibility, and perhaps try to repair the solution if it is not feasible.
Today's question involved a warm start that the author was confident was feasible, but that CPLEX was asserting was not (message: "Retaining values of one MIP start for possible repair"). I've seen essentially the same question other times, sometimes with the "retained for repair" message and sometimes with a flat-out rejection. What can you do if CPLEX disagrees that your starting solution is feasible?
First note that the more complete the starting solution, the easier it is for CPLEX to digest it. If you specify, say, values for only the integer variables, CPLEX will try to solve for the corresponding values of the continuous variables. That's usually relatively painless, although (as with anything else MIP-related) your mileage will vary. If you specify values for just a portion of the integer variables, though, repairing the starting solution turns into a MIP problem unto itself. I'm pretty sure it is rarely the case that a warm start that incomplete will pay any dividends, even if CPLEX manages to repair it.
There is a parameter (MIP.Limits.RepairTries) that governs how much effort CPLEX spends trying to repair a starting solution. Higher values lead to more time spent trying to fix your warm start. The author of today's question had that cranked up quite high, so he needed to look other places.
You may be convinced that the warm start you are supplying is feasible, but sometimes bugs happen, or a bit of rounding bites you in the sitzfleisch. A useful thing to try is fixing all the variables (or at least all the integer variables) to match the starting solution, by setting both the lower and upper bound of each variable to its value in the warm start. In effect, you collapse the feasible region down to a single point. Now tell CPLEX to solve the model. If it comes back immediately with your starting solution as the optimal solution, then your warm start really is feasible. On the other hand, if CPLEX claims the problem is now infeasible, run the conflict refiner and get a set of constraints that CPLEX feels are mutually inconsistent. Check your starting solution against those constraints manually and look for a discrepancy.
Update: It turns out that there is an API function (IloCplex.refineMIPStartConflict in the Java API, various pseudonyms in other APIs) that lets you skip the "fix the variables" step and directly identify a conflict in the starting solution (if, in fact, one exists).
One other possibility is numerical instability in the model (basically the MIP version of "gremlins"). Solve the model (without fixing any variables as described in the previous suggestion) and collect information on basis condition numbers. I've covered that subject before ("Ill-conditioned Bases and Numerical Instability"), so I won't rehash it here. If you model is unstable, small rounding errors in your warm start can blow up into deal-breaking errors in constraint satisfaction. There is a parameter (Emphasis.Numerical) that tells CPLEX to spend extra effort on numerical precision, but the more general approach to instability is to look for reformulations of the model that are more stable. In particular, avoiding a mix of large and small constraint coefficients (such as is commonly induced by the dreaded "big M" method of formulating logical constraints) may be helpful.
It is possible to "warm start" CPLEX (and, I'm pretty sure, at least some other solvers) by feeding it an initial solution, or a partial solution (meaning values for some but not all variables). CPLEX will try to complete the solution if necessary, test for feasibility, and perhaps try to repair the solution if it is not feasible.
Today's question involved a warm start that the author was confident was feasible, but that CPLEX was asserting was not (message: "Retaining values of one MIP start for possible repair"). I've seen essentially the same question other times, sometimes with the "retained for repair" message and sometimes with a flat-out rejection. What can you do if CPLEX disagrees that your starting solution is feasible?
First note that the more complete the starting solution, the easier it is for CPLEX to digest it. If you specify, say, values for only the integer variables, CPLEX will try to solve for the corresponding values of the continuous variables. That's usually relatively painless, although (as with anything else MIP-related) your mileage will vary. If you specify values for just a portion of the integer variables, though, repairing the starting solution turns into a MIP problem unto itself. I'm pretty sure it is rarely the case that a warm start that incomplete will pay any dividends, even if CPLEX manages to repair it.
There is a parameter (MIP.Limits.RepairTries) that governs how much effort CPLEX spends trying to repair a starting solution. Higher values lead to more time spent trying to fix your warm start. The author of today's question had that cranked up quite high, so he needed to look other places.
You may be convinced that the warm start you are supplying is feasible, but sometimes bugs happen, or a bit of rounding bites you in the sitzfleisch. A useful thing to try is fixing all the variables (or at least all the integer variables) to match the starting solution, by setting both the lower and upper bound of each variable to its value in the warm start. In effect, you collapse the feasible region down to a single point. Now tell CPLEX to solve the model. If it comes back immediately with your starting solution as the optimal solution, then your warm start really is feasible. On the other hand, if CPLEX claims the problem is now infeasible, run the conflict refiner and get a set of constraints that CPLEX feels are mutually inconsistent. Check your starting solution against those constraints manually and look for a discrepancy.
Update: It turns out that there is an API function (IloCplex.refineMIPStartConflict in the Java API, various pseudonyms in other APIs) that lets you skip the "fix the variables" step and directly identify a conflict in the starting solution (if, in fact, one exists).
One other possibility is numerical instability in the model (basically the MIP version of "gremlins"). Solve the model (without fixing any variables as described in the previous suggestion) and collect information on basis condition numbers. I've covered that subject before ("Ill-conditioned Bases and Numerical Instability"), so I won't rehash it here. If you model is unstable, small rounding errors in your warm start can blow up into deal-breaking errors in constraint satisfaction. There is a parameter (Emphasis.Numerical) that tells CPLEX to spend extra effort on numerical precision, but the more general approach to instability is to look for reformulations of the model that are more stable. In particular, avoiding a mix of large and small constraint coefficients (such as is commonly induced by the dreaded "big M" method of formulating logical constraints) may be helpful.
Tuesday, May 12, 2015
Hell Hath No Fury Like a Dependency Scorned
There is a recent package for the R statistics system named "Radiant", available either through the CRAN repository or from the author's GitHub site. It runs R in the background and lets you poke at data in a browser interface. If you are looking for a way to present data to end-users and let them explore the data dynamically, rather than looking at a bunch of static plots, you might find radiant rather useful.
So I set out to install it, first on my PC and then, when that failed, on my laptop. If you look at the CRAN page, you can see which other R packages radiant requires. That's interesting but not terribly crucial, since the R package installation system by default handles dependencies for you.
The problem is that the package installer will compile radiant, and its various dependencies, on your system, or in my case die trying. What is not visible (with radiant or any other R package) is which non-R compilers and libraries are required. As it turns out, beyond the usual suspects (mainly gcc, the GNU C++ compiler, which I think is a given on pretty much every Linux installation), radiant (or some of its dependencies) requires the GNU FORTRAN compiler (gfortran), which I had on my PC but not my laptop. That much was easy to figure out.
Harder to understand were compilation error messages for some of the dependencies saying "cannot find -lblas" and "cannot find -llapack". For the nontechnical user, even finding those messages in the torrent of compiler output might be a bit iffy. As it happens, I know enough (just barely) to know that "-l" is a prefix telling the compiler to load a library and "blas" and "lapack" were the library names. As it happens, I even know that "blas" is the Basic Linear Algebra Subprograms library and "lapack" is the Linear Algebra Package library. What I did not know was why the compiler could not find them, given that both libraries are installed on both machines.
Trial and error yielded an answer: the compiler needs the static versions of both. Rather ironically, the Wikipedia entry for static libraries (the immediate preceding link) lists one advantage of static libraries over their dynamic counterparts (the ones I already had installed) as "... avoid[ing] dependency problems, known colloquially as DLL Hell or more generally dependency hell". Little do they know ...
Anyway, on Linux Mint (or, presumably, Ubuntu), you can find them listed in the Synaptic package manager under "libblas-dev" and "liblapack-dev". Install those first (along with "gfortran" if not already installed) using Synaptic or apt (from a command line), then install radiant and its dependencies from CRAN using R, and things should go fairly smoothly. For Windows or Mac users, you'll need the same two libraries, but I'm afraid you're on your own finding them.
So I set out to install it, first on my PC and then, when that failed, on my laptop. If you look at the CRAN page, you can see which other R packages radiant requires. That's interesting but not terribly crucial, since the R package installation system by default handles dependencies for you.
The problem is that the package installer will compile radiant, and its various dependencies, on your system, or in my case die trying. What is not visible (with radiant or any other R package) is which non-R compilers and libraries are required. As it turns out, beyond the usual suspects (mainly gcc, the GNU C++ compiler, which I think is a given on pretty much every Linux installation), radiant (or some of its dependencies) requires the GNU FORTRAN compiler (gfortran), which I had on my PC but not my laptop. That much was easy to figure out.
Harder to understand were compilation error messages for some of the dependencies saying "cannot find -lblas" and "cannot find -llapack". For the nontechnical user, even finding those messages in the torrent of compiler output might be a bit iffy. As it happens, I know enough (just barely) to know that "-l" is a prefix telling the compiler to load a library and "blas" and "lapack" were the library names. As it happens, I even know that "blas" is the Basic Linear Algebra Subprograms library and "lapack" is the Linear Algebra Package library. What I did not know was why the compiler could not find them, given that both libraries are installed on both machines.
Trial and error yielded an answer: the compiler needs the static versions of both. Rather ironically, the Wikipedia entry for static libraries (the immediate preceding link) lists one advantage of static libraries over their dynamic counterparts (the ones I already had installed) as "... avoid[ing] dependency problems, known colloquially as DLL Hell or more generally dependency hell". Little do they know ...
Anyway, on Linux Mint (or, presumably, Ubuntu), you can find them listed in the Synaptic package manager under "libblas-dev" and "liblapack-dev". Install those first (along with "gfortran" if not already installed) using Synaptic or apt (from a command line), then install radiant and its dependencies from CRAN using R, and things should go fairly smoothly. For Windows or Mac users, you'll need the same two libraries, but I'm afraid you're on your own finding them.
Subscribe to:
Posts (Atom)