Separable Benders Decomposition

A reader (I have readers??) asked me a question about Benders decomposition of a mixed-integer program (MIP) when the linear program (LP) subproblem is decomposable: how do we glue together a mix of optimality and feasibility cuts from the subproblems? The short answer is that we don't.

Rather than repeat a lot of definitions, I'll just refer you to a previous post for some background (if you need it; chances are you don't, because if you're not familiar with Benders, you've already tuned out). I will repeat the formulation of a generic decomposable MIP, just to establish notation:\[ \begin{array}{lrclcc} \textrm{minimize} & c_{1}'x & + & c_{2}'y\\ \textrm{subject to} & Ax & & & \ge & a\\ & & & By & \ge & b\\ & Dx & + & Ey & \ge & d\\ & x & \in & \mathbb{Z}^{m}\\ & y & \in & \mathbb{R}^{n} \end{array} \]The MIP decomposes into a master MIP (containing \(x\) and a real variable \(z\) that serves as a surrogate for \(c_{2}'y\)) and a subproblem (LP) containing \(y\).

Now suppose that \(B\) and \(E\) are both block-diagonal, with the same block structure and with \(K\) blocks. We can decompose the subproblem into \(K\) smaller LPs. In the master problem, we replace \(z\) with \(z_1+\dots+z_K\), with \(z_k\) the surrogate for the objective contribution \(c_{2k}'y_k \) from the \(k\)-th subproblem.

When we obtain an incumbent solution \((\hat{x},\hat{z}_1,\dots,\hat{z}_K)\) in the master, we pass \(\hat{x}\) to each subproblem and solve. Some subproblems may be infeasible (generating feasibility cuts); others may have optimal solutions with \(c_{2k}'y_k\gt\hat{z}_k \) (in which case we generate an optimality cut); and some may have optimal solutions with \(c_{2k}'y_k=\hat{z}_k \), requiring no action. If any subproblem is infeasible, then \(\hat{x}\) is infeasible in the original problem regardless of what goes on in other subproblems, and the feasibility cut from the subproblem is a valid feasibility cut in the master. Similarly, if \(\hat{z}_k\) underestimates the objective value in subproblem \(k\), then the optimality cut generated there is valid in the master regardless of what happens in other subproblems. So each feasibility/optimality cut generated in a subproblem can be added to the master problem without modification. There is no need to combine cuts (and, in fact, combining cuts might weaken them).

I'll close with two comments. First, although Benders is usually taught as "solve master, solve subproblem, add one cut, repeat", adding multiple cuts during one iteration is certainly legitimate and possibly beneficial (assuming, as in this case, that you discover multiple valid cuts). The cuts need not all be a single type (optimality or feasibility); a mix is perfectly fine. Second, while it is fine to solve every subproblem at every iteration, you may also opt to solve the subproblems in some order (perhaps cyclical?), abort the cycle the first time a subproblem generates a cut, and add just that one cut. This speeds up each cycle but delays finding cuts. I really do not know which way is better, but I suspect that optimality cuts generated from a value of \(\hat{x}\) that is found to be infeasible in another subproblem may not be all that useful, and multiple feasibility cuts lopping off the same \(\hat{x}\) might be a bit redundant. So I would be inclined to abort the cycle the first time I got a feasibility cut, and add just that cut, but add all the optimality cuts I found if no feasibility cut was generated.

Boot Bug: Anniversary Edition

A year ago July, I ran into a problem in which my AMD-64 Mint Katya system started to hang on boots. As noted in that post, the problem stemmed from messing with the video settings for the boot loader. Reinstalling the nVidia display driver might or might not have helped eliminate the problem, but eventually it sorted itself out.

A month later, I ran into a second problem linked to the nVidia driver, in which the X server decided to spontaneously reboot on occasion. I got rid of that problem by using the sgfxi script to update to the latest version of the nVidia driver.

Do gremlins celebrate anniversaries? Slightly over one year after fixing the second problem, the first one came back. It started when I tried to run a program that crashed because it could not find a way to do XGL hardware graphics acceleration. That led me to the Additional Drivers dialog in the Control Center, where I discovered that the proprietary nVidia driver was not selected. As it turns out, that's probably because the Control Center sees the one the operating system installed but not the newer one that the sgfxi script installed. I'm not sure that either version was running, though, since both should provide XGL.

Anyway, I decided to turn on the proprietary driver in the Additional Drivers dialog. When I rebooted, the machine hung at the battery test stage. (Note to self: if this happens again, do not turn on the proprietary driver. Get out of X and run the sgfxi script.) I could boot into safe mode, but no way could I boot regularly (despite repeated attempts). Safe mode worked, but it used too low a resolution, with the desktop off-center (left edge cut off, blank screen on the right), and I could not change the resolution. In Control Center > Monitors I discovered that the system could not detect what kind of monitor I had, so it gave me a wimpy default choice that I could not edit.

Eventually I booted into safe mode, went back to Additional Drivers and discovered that I now had a new option: an "experimental" driver. This was the nouveau driver, which I selected. With the nouveau driver, I could boot normally and get to the desktop, but the resolution was still wrong, and the desktop was still off-center. So I switched back to the nVidia driver, and the next boot predictably hung.

I booted into safe mode again, but this time I selected the option to repair packages, thinking perhaps one of the X packages was damaged. That was apparently not the case, but it did remind me that I had seven updates I had not installed. These were updates to the Linux core, including the X system. Normally I don't install those updates because I like to upgrade to a new version of the entire system at once. This was not a normal time, though (particularly as it was getting on 1:30 in the morning), so I let the system install the updates and rebooted again ... and everything worked. Mint automatically detected my monitor correctly, the resolution was set correctly, everything was back the way it had been.  As an added bonus, the nVidia driver was being used, and the program that triggered this whole cluster worked correctly. Woo-hoo!

I subsequently ran the sgfxi script, and sure enough I was on a one-iteration-old nVidia driver. I let the script upgrade me to the latest version, and everything still seems to work properly.

There won't always be a core update waiting to bail me out, so I guess the solution process next time (a year from now?) will be as follows:

1. Try the sgfxi script.
2. If that fails, see if there's an update to any of the X packages that can be installed. If not, try reinstalling the X system.
3. If that also fails, swear mightily and see if there's a new version of Mint I can download.

Streaking - Automotive Edition

If you came here expecting something about driving around nekkid, sorry to disappoint you: that's not the theme of this post. (Trust me when I say that nobody wants to see a guy my age tooling around in the buff.) This post is about cleaning car windows.

Among the many things I'm not good at (a very long list), washing car windows is a prominent item. I've tried glass cleaners, bleach-based cleaners, soap-and-water, plain water, even windshield washer solvent, and inevitably the windows end up with streaks. A bit of research turned up the fact that there are special purpose sprays, allegedly used by people who "detail" cars. I'm not that anal (and too cheap) to buy them. Fortunately, I've had a bit of luck recently, which I'm writing down here so that I won't forget it.

As a starting point, if the windows are really grungy, it's probably a good idea to wash off the bulk of the dirt with plain water, blotting stuff up with paper towels so that you don't leave mud caked on the windows. (Between endless road construction and my driving with the sun roof open, this is a nontrivial consideration, both exterior and interior.)

Next comes the secret elixir: vinegar and water. I read someplace that white vinegar works best, but I've been getting good results with apple cider vinegar, which is what I happen to have in the kitchen. The exact proportions of the mixture are a mystery to me, but I think it's safe to say more than half should be water. (Note to self: less vinegar next time. We're not making salad dressing.)

The other key tool is newspaper. For whatever reason, newpaper works better than even paper towels at both absorbing the dirt and not leaving streaks. I worried at first that the ink would bleed onto the windows, but that does not seem to be the problem. After a few brief experiments, it appears that (as with other uses) the New York Times does better than my local paper, but either will work. I'm not sure if really conservative papers will work as well; they may insist that you outsource the job. In any event, you'll want to read the paper before washing the windows with it.

One or two web sites talked about devoting a spray bottle to applying the mix, but that strikes me as overkill. Wad up one sheet of newsprint, dip one end in a bowl of the mix, and apply it. Wipe, and use the dry end to blot up any excess. Repeat as needed.

The results are not perfect, but they're better than anything I've achieved in the past.

Big (?) Ideas for 2012

With the start of the school year (for some people :-)), Aurelie Thiele is back and blogging again, starting with a post about some of the themes from the annual “big ideas” issue of "The Atlantic". I'm not sure exactly how big these ideas are, and the meritocrat in me disagrees with the third one (lotteries for college admissions), but the first two certainly resonate, as does the fourth (hire introverts -- believe it or not, according to the Myers-Briggs Type Indicator, I'm one). The first two resonate in part due to person experiences.

The right to be forgotten: This pertains to the ability of an individual to insist that old elements of their Internet "footprint" be deleted. There's no easy answer here: the right to privacy, free speech, censorship, domestic and international law are all tangled up in this. There is, however, one fairly straightforward partial answer: assume that anything you put out on the Internet is out there permanently. Hence, if something strikes you as potentially embarrassing, don't do it.

Case in point: quite a few years ago I taught a course in business use of the Internet, which included the basics of creating and maintaining a web site, including HTML and producing dynamic pages (using Cold Fusion). During the course, students did a series of homework assignments that created a personal web site (hosted on a university server). I warned them, day one, that anything they posted was visible to the networked portion of the planet, and that they should accordingly avoid anything embarrassing. One of the assignments was to a create a web form. The context of the form was up to them, so long as it met reasonable standards of decency, but the form had to have at least one of every HTML form element (radio buttons, text fields, a password field, ...).

One young lady created a form that I think had something to do with how the respondent spent his/her free time. One of the questions was "How many people have you murdered lately?" It was obviously intended to be humorous. I cringed internally a bit, but it met the standards of the assignment, and so I accepted it.

Not too long after the student graduated, I got a somewhat frantic message from her. She was interviewing for a position with a company, and as part of their vetting process they routinely looked people up on search engines. So she did a Google search for her own name and found her old course web site ... including the aforementioned form. Her immediate concern was how to get the site taken down from the university server, but as I pointed out to her, search index entries can outlive the sites they index, and back then Google kept cached copies of sites. (I'm not sure if they still do.) I explained the general mechanics of getting a site deleted from a search index -- the specifics vary from one engine to the next -- and wished her luck. I'm pretty sure at that point she was regretting her choice of questions for the form.

Boot camp for teachers: The gist of this idea is that practice teaching, in a simulated classroom environment (including simulated students), is the best way to prepare for the unpredictability of an actual classroom.

I was a graduate teaching assistant in mathematics during my doctoral program. Our department scheduled an orientation for new TAs prior to the start of fall term. As part of it, each of us had to prepare a lesson (for the freshman pre-calculus algebra course) and deliver it to a room full of professors, senior doctoral students and our fellow new fish. The professors and senior doctoral students played the roles of freshmen attending the course, and the senior doctoral students took particular pleasure in simulating undergraduate student behavior to the best of their ability. (Happily, this was before smart phones existed.)

I recall one new TA running through an algebra lesson when a simulated student (one of the older doctoral candidates) interrupted him: "Why?" The teacher-to-be launched into some calculations, which the "student" promptly interrupted with another "Why?"  As the new TA broke the calculation down into smaller and smaller steps, his tormentor questioned each one with that same three letter interrogative ... until finally a clearly exasperated TA blurted out "Because that's how God made the real numbers!"

Possible theological concerns aside, that is not likely to be an answer that would satisfy a real student. Moreover, as we new people eventually learned, part of teaching is classroom management -- you can't drop too much time on one question, unless perhaps the entire class is stuck on it, and if you focus too much on one student the others may tune out. A carefully worded variant of "see me after class" may be the best response to the situation being simulated, a very realistic albeit slightly exaggerated scenario.

Having sat through that, and looking back on my own teaching career, I can definitely say that a healthy dose of simulated teaching can head off some potentially significant classroom problems. In fact, I would have benefited from more than that one session, although at the time I doubt I would have appreciated the extra training.

Phantom Recordings Vaporized

As I mentioned in my previous post, a rather odd problem with network ports and IPv6 addressing broke my Mythbuntu installation. I've since confirmed that the fix I reported is working. At one point during the breakdown I tried to record an episode of the TV series "Perception" title "Kilimanjaro". When the recording failed, I rescheduled it ... once. That somehow led to approximately 1,100 entries for "Kilimanjaro" in the list of recorded shows, all with a size of either zero or one byte. Not only did that clutter the list, it significantly slowed  MythTV's display of the list, not to mention some other functions. The phantoms had to go.

I knew that MythTV stores all sorts of records in a MySQL database. A bit of searching turned up this post, which told me what I needed to know: that I could delete entries from the recorded table without breaking the database. So I installed MySQL Navigator, pointed it at the mythconverg database, and got to work. The database name, user id and password (along with host name and port) are all stored in ~/.mythv/config.xml. Once into the database, I ran

select * from recorded

to get the lay of the land, then

select count (*) from recorded

to get the total number of entries and 

select count (*) from recorded where subtitle = 'Kilimanjaro'

to get the number of phantom entries. The point of this was not just to satisfy my curiosity; I wanted to be sure that my next query would not delete everything. The third select helps me confirm that my "where" clause will do the right thing. (I tend to be cautious when deleting or updating database records.) Finally, it was time to do the deed:

delete from recorded where subtitle = 'Kilimanjaro'

nuked the phantom entries.

(As a quick sidebar, learning SQL, and specifically the MySQL version, has paid dividends for me over the years. For anyone doing operations research software development, whether personal or professional, and for anyone doing web development, it's a great investment of time.)

Deleting entries in the recorded table does not delete any actual recordings, and I wanted to be sure that there were no files associated with the phantoms. I also wanted to make sure that there were no live TV recordings sitting around. (The recorded table also showed a 10 second live recording from the day that I installed Mythbuntu and tested its functionality. That entry was another phantom, which I deleted.) So I went to check the directories where MythTV stores files. I started by looking in obvious places, to no avail. I then did a web search, which provided several widely differing answers, some specific to Mythbuntu and some generic for MythTV, and all of them wrong! So it was back to manual search. For the record, I found the files under /var/lib/mythtv (live recordings in the livetv directory, taped shows in the recordings directory).

Mythtery Solved?

Previously, I described a problem with my Mythbuntu installation that developed suddenly on August 24 (meaning that the system worked fine from installation this past May through August 23, then stopped working on the 24th). The symptom was a failure by the front end (and by the Mythwelcome application) to connect to the back end. It seemed possibly to have something to do with using IPv6 rather than IPv4, specifically on the wireless LAN connection. I won't repeat all the gory details but instead refer you to the previous post (if you care).

To understand both the problem and what appears to be the solution (knock on virtual wood), you have to know a bit about my setup. I have a PC dedicated to recording and replaying TV. The front and back ends of MythTV are both on that box. The box has three network connections:

• eth0 is a built-in (and unused) Ethernet port;
• eth1 is a Hauppauge WinTV-DCR external TV tuner, connected via USB; and
• wlan0 is a wireless network adapter, connecting the PC to my home WiFi network (I have DSL service with a DSL modem that also serves as gateway and WiFi router).

After wearing out Google trying to find solutions, I came across something that made me think that turning off both Ethernet ports would resolve the problem. I'm not sure why it would, given that error messages in the back end log typically referred to problems with wlan0, but I gave it a try. In a sense it worked: with both Ethernet ports disabled, the front end had no problem talking to the back end. Unfortunately, disabling eth1 meant that the back end could not see the tuner card, so it would dutifully wake the PC at the designated time and try to record a show, but fail miserably (and silently). Disabling just eth0 was not enough; the front end and back end were again not on speaking terms.

After more adventures with Google, including the discovery of a proposed workaround in this bug ticket, I found a combination of things that seems to have worked. On three successive reboots the front end has been able to converse with the back end, I have been able to schedule recordings, and the PC can see the tuner. I've yet to actually record something, but I'm cautiously optimistic.

I don't know if all the following steps are necessary, and I'm not going to experiment further unless the system breaks again. What I did was:

• disabled IPv6 as described in the bug ticket (which, from experience, was not sufficient in and of itself);
• assigned the wireless connection on the PC (wlan0) a static IP address within the range supported by my DSL modem;
• ran the back end setup program and changed the IP address of both local and master back ends (which are the same in my case) to that static IP address; and
• changed the IPv6 settings for both eth0 and eth1 from "automatic" to "ignore".

I have no problem with having to disable IPv6; it's not as if my home WiFi network is going to run short of addresses with IPv4. I don't know why the last step was necessary given the first step, but from experience it was. I don't know if the first step is necessary given the last step. Basically, my answer to any question about this (after being stripped of expletives) is "I don't know". I just hope the fix holds up.

That leaves me with one mildly annoying problem. During the period where the front and back ends were not communicating, MythTV failed to record a few scheduled programs. One of them appears in the list of recorded shows with a size of 1 byte. This by itself is not the issue. What's annoying is that it appears in the list 1,100 times! Or at least it did: I've gotten it down to a bit over 1,000 by manually deleting the entries one at a time. I'm hoping there's a clever and much more efficient way to get rid of the rest. Ordinarily I'd crank up the MySQL command client and run a delete query on the database, but the MythTV database has quite a few tables, I'm not sure what all I would have to delete, and I really don't want to mess up the database.

Microsoft Academic Search: Randomization in Action?

Move over, Google Scholar! Microsoft has apparently decided to join the scholarly search fray with Microsoft Academic Search (MAS). The page (whose logo indicates it is in beta test) allows you to search for papers and authors and find all sorts of fascinating (to the author's mother) information ... about someone who may or may not be her offspring.

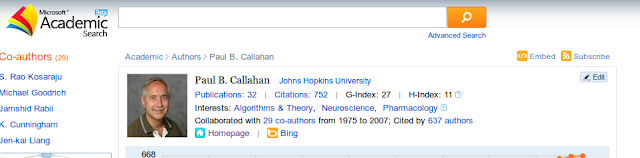
I discovered this when someone sent me an email message expressing confusion about my relationship to "Paul B. Callahan". Trust me, his confusion was dwarfed by mine, as I've never heard of Mr. (Dr.?) Callahan. The author of the email included a link to this page on MAS. Since the page is likely to change in the future, I'll embed a snapshot below.

That is in fact my smiling face next to Dr. Callahan's name, and the "Homepage" link does take you to my home page. In addition to the difference in names, I have never been at Johns Hopkins University (which I'm sure comes as a relief to them), I know next to nothing about neuroscience, and I skipped the pharmacological portions of the '60s and '70s.

So I tried searching MAS for "Paul A. Rubin" and ended up here. Again, I'll include a screen shot.

The picture might be me if taken in very low light, and once again the homepage link is to my home page. My association with George Mason University is much like my association with Johns Hopkins University: nonexistent. (For future reference, I have no association with any university whose school name is or sounds like the first and last names of a person.) "Business Administration and Economics" might fit me, to the extent that some of my publications are in journals that fall in that category (and I did teach in a business school), but nuclear physics and nuclear energy are a major mismatch. My parole office won't let me have a slingshot, much less get near anything fissile. For that matter, I'm wondering if the PAR at GMU (if one really exists) actually has one foot in business and another in nuclear anything. (I say "another" and not "the other" because playing with nuclear stuff has been known to cause mutations.)

If you examine the list of publications on that second page, some are mine and some are very much not.

I searched the site for instructions on how to report errors. The answer is that you do not report them; you edit them out yourself. I have no idea if this means that anyone with an account can edit these pages (what could possibly go wrong with that?), or if the "owner" has to edit the page (in which case who owns the second one, me or my doppelganger at GMU?). In any event, I have no intention of creating an account with Microsoft just so that I can clean up their errors.

If I could edit the pages, I'd be tempted to change my photos into links to Google Scholar. So probably MS is just as happy that I'm not setting up an account.