My first reaction was "No fooling!" (Actually, "fooling" is an editorial substitution. I can be a bit cranky when I'm torn from the arms of Morpheus.) Hot on that first reaction was this: "The normal density is not a fractal." Specifically, the right tail of a bell curve is not itself a bell curve ... and if I can recognize that while half asleep, it must be fairly obvious. So where's the beef?
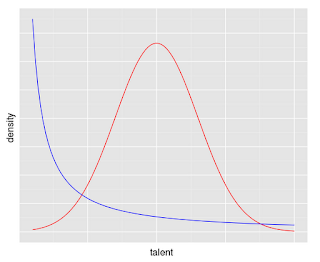
The first figure below shows density functions for Gaussian (red) and Pareto (blue) distributions. The second figure shows a plausible Gaussian distribution for athletic ability among the overall population. Professional athletes, or Division I collegiate athletes, presumably fall in the right tail (shaded). The right tail bears considerably more resemblance to the Pareto distribution in the first figure than it does to a Gaussian distribution.
The research documented in the paper covered five studies (one for each of the fields I listed above) using 198 samples (a variety of performance measures for each field, or subsets of each field), involving a total of 633,263 individuals. As with any statistical study, you can question methods, sample definitions, interpretation of results etc. I've read the paper, and I find the evidence fairly compelling, particularly as it confirms my initial intuition (expressed in my waking reaction).
I'm not sold on Pareto as the correct choice among one-tailed distributions, and I'm not sold on single tail distributions in general. Consider, for instance, a performance measure on a [0,1] scale, such as career batting average for baseball players. The bounded domain precludes a long, thick tail on either side. A friend of mine did in fact download and fit some batting average data. I won't reproduce it here, since I'm not sure how his sample was defined (all players or just selected ones), but the histogram he showed me was a lot closer to Gaussian than to Pareto.
That said, it seems intuitive to me that if performance correlates strongly to ability, if ability has a roughly Gaussian distribution, and if there is a selection mechanism in play that selects the most able to compete, then performance among the competitors will not be Gaussian. This needs to be qualified in a variety of ways, including the following:
- Not everyone with high ability may choose to compete. Athletes may find it more lucrative (and less dangerous) to act in adventure films; people capable of great research may find it more lucrative to work in industry (where opportunities to publish are greatly diminished).
- Not everyone with high ability may have the opportunity to compete. Some star athletes are forced to retire prematurely, or to abandon hope of starting a professional career, due to health concerns. Potential stars in any field may go undiscovered due to where they live or what schools they attend. At the risk of creating a distraction by introducing a somewhat charged topic, women or members of an ethnic (here) or religious (elsewhere) minority may be excluded or discouraged from entering the competition, regardless of their ability.
- Nepotism (particularly but not exclusively in the entertainment field) may introduce competitors who do not reside in the right tail of the ability distribution. To a lesser extent (I think), diligence, hard work or "heart" may allow some people with above median but less than excellent athletic ability to compete in high level events.
- Productivity is not always a monotonic function of talent. A very talented wide receiver may not catch many balls if he is on a team with a relatively poor quarterback, a strong running game, and/or a stellar defense (allowing the team to practice a conservative offense). Conversely, a modestly talented receiver on a team with no running game and a poor defense (so that they are perpetually playing catch-up) may catch a disproportionate number of passes. Similar things can happen to an academic with great research potential working at a "teaching school", or in a department lacking resources and not providing colleagues or doctoral students with whom to collaborate. (Conversely, some faculty are adept at riding the coattails of their more productive colleagues, showing up as coauthors of all sorts of papers.)
Now it is not the case that the response variable (here, the performance measure) need be normally distributed in order for the residuals to be normally distributed. Unless ability is adequately covered by the explanatory variables, though, the effects of ability will be seen in the residuals, and if the distribution of ability among the sample (those who likely were chosen at least in part on the basis of ability) bears any resemblance to a Pareto distribution, it seems fairly unlikely that the residuals will be normally distributed ... and fairly risky to assume that they are. Some academic papers cite specific tests of the normality of residuals, but in my experience it is far from a universal practice.
The authors of the paper point out a second issue related to this. Extremely high values of performance are more likely to occur with Pareto distributions than with Gaussian distributions. Some (many?) authors, taking normality for granted, treat extreme values as outliers, assume the observations are defective, and "sanitize" the data by excluding them.
So consumers of academic papers studying performance may be buying a pig in a poke.
[1] O'Boyle Jr. and Aguinis, "The Best and the Rest: Revisiting the Norm of Normality of Individual Performances." Personnel Psychology 65 (2012), 79-119.

I have two comments:
ReplyDelete1) In the figure, it looks as if there was a hard threshold, where people with a certain ability enter the sample of athletes. In your explanation, however, you state various reasons why this threshold may well be a quite individual one, in which case you may actually return to having a normal distribution, even for athletes. Then, the bell curve may not be a fractal, but due to sample selection behave just like one. Now this is ability of athletes, but the issue was performance.
2) Performance is not the same as ability and as you already stated, you probably need to include personal chances as explanatory variable of performance. Assuming personal chances to be normally distributed, if we multiply both random variables, we obtain the normal product distribution, which looks a lot like a Pareto distribution.
Nils,
ReplyDeleteOn your first point, I think the "leakage" in the low end threshold might be enough to produce an initial upward trend in the density of the performance measure, but I doubt it is enough to produce a density close to the normal (and, in particular, that it would be enough to offset the "heavy tail" effects reported by the authors of the paper). That's pure speculation on my part.
Your second point is well taken, although I'm not sure that the two distributions you would be convolving would both be normal. If you are correct about arriving at something like a normal product distribution, it still confirms the authors' concern about assuming normality in regression residuals.
Thanks for the comment!
That was a lot of “ifs” there, in paragraph 6! In addition to the practical issues you identify in your bullet points, there is also the fact that in many (most?) endeavors, ability is not unidimensional. So the selection mechanism you mention will most likely give you some individuals who are not particularly close to the right-hand tail on one dimension of ability, but who are selected because they excel in a different dimension – the speedy receiver vs. the “sure hands” receiver vs. the receiver who can take a hit and advance the ball. I suspect this will also introduce more of a left tail in the distribution of performance.
ReplyDeleteAs regards the findings in the P Psych paper in particular, I think there’s an issue with the measures considered. You use the term “productivity” in your post as more-or-less a synonym for “performance.” The authors of the P Psych paper stick mainly to “performance,” but in their discussion of the importance of their findings, they use “productivity” extensively. Economists (sorry) define productivity as output per unit of input. To properly compare the productivity of different “producers,” you need comparable output measures and comparable input measures.
My concern with the measures examined in the P Psych paper is that most are cumulative “career” totals (total hits, total yards, total nominations, total elections won, etc.). The denominator – “career” – is going to represent vastly different numbers of “opportunities” across the individuals in the population. In some categories, even individuals whose careers are the same duration will have more minutes played, passes attempted, at-bats, etc. Moreover, for many of the measures they consider, “success” begets more opportunities (you get more playing time or whatever), which adds to the long right tail phenomenon.
The batting stats I sent you earlier are for the 2011 Major League Baseball season, and cover the 145 players who qualified for the batting title in their respective leagues (a minimum of 502 plate appearances). So in a sense, this is an even more elite group of players than the Majors as a whole.
For this group, Total Hits is clearly non-normal, with a long right tail, but definitely has a left tail, too. On Base Percentage and Batting Average, which are both “per opportunity” measures pass K-S and Wilk-Shapiro tests (.05 level of significance) for normality. They aren’t perfect bell curves, but they’re nothing close to a Pareto distribution.
I’m not trying to suggest that productivity is necessarily normally distributed, but I do think that the findings in the P Psych paper are largely an artifact of the measures the authors chose to examine.
G -
DeleteGood think I included figures, or your comment would be longer than my post! Also, -1 for moving from I/O psych (already fuzzy enough) to economics (even fuzzier?).
The point about multiple ability dimensions is apt. I suspect that in a lot of cases (athletics, music, ...), the "chosen" are better than the rest of us on pretty much all important ability dimensions, but among themselves there may not be a clear dominance relations. If we collapse multiple ability dimensions to a single scale, say with some sort of weighted average, it's possible that among the chosen the distribution of the composite score is less Paretian and possible even plausibly normal.
Your point about career totals versus averages is interesting, but I'm not sure it contradicts the conclusions of the authors. If success begets more opportunities, which in turn begets more success, that would certainly thicken the right tail, but it wouldn't eliminate the left tail, nor would it necessarily be the sole source of thickness of the right tail.
As far as OBP and BA go, my comment in the second paragraph below the plots applies to them: they're on a [0,1] scale, so they pretty much can't have a right tail thick enough to fit a Pareto distribution. (Pareto distributions tend to have lots of extreme values, and consequently large means.) I'm not positive, but I think the only way you could get a fit to a Pareto distribution with one of them would be if a *lot* of players *never* got a hit or got on base (which might discourage their employers from putting them in the lineup). The key question (for which I lack an answer) is whether they pass the K-S and W-S tests because they're plausibly normal or because those tests lose power when dealing with unimodal distributions with fairly compact support.
The authors of the paper were pointing toward studies that look at worker productivity/performance/whatever, though, and so I think you have a fair criticism of their choice of career statistics for their tests. Separate from your statistical concerns, I think the studies they are indirectly criticizing typically look at annual performance measures, so it would be more apples-to-apples if they had used annual measures in their tests.
"As far as OBP and BA go, my comment in the second paragraph below the plots applies to them: they're on a [0,1] scale, so they pretty much can't have a right tail thick enough to fit a Pareto distribution."
DeleteFor the 2011 season, OBP in the sample of 145 I looked at ranged from .248 to .448. Batting average ranged from .218 to .344. There's plenty of room for someone(s) to thicken the right tail of the distribution. Artificial truncation isn't really the issue.
"I'm not positive, but I think the only way you could get a fit to a Pareto distribution with one of them would be if a *lot* of players *never* got a hit or got on base"
I think if there were a *lot* of players who had a batting average of .218 and few or none below (like the figure in your original post would suggest), you could probably get a pretty good fit.
I did a MLE fit of a Pareto distribution to the batting averages. (Thanks for the data.) The minimum of the fitted distribution's support equals the sample min (0.218 here), so the fitted distribution is obviously not totally accurate (Mario Mendoza's lifetime BA was .215), but it's close enough for estimating tail thickness.
DeleteThe fitted distribution would assign a probability of 0.061 to batting .400 or higher (lookout Ted Williams!), 0.0094 to batting .600 or higher (which, given the number of major leaguers, would mean it should have been done by now), 0.0025 for batting .800 or higher, and a tad under 0.0009 for batting 1.000 or higher (good luck with the "higher").
The usual rationale for using normal distributions when we know the variable has a finite domain is that the portion of the tails outside the variables true domain has negligible probability. My point about fat tails for the Pareto is that the right tail probably doesn't die fast enough to let you make that assumption about averages, and I think the probabilities I just cited are sufficiently nontrivial to support my point. For "unbounded" variables (lifetime hits, lifetime stolen bases, or for Earl Weaver lifetime ejections), a Pareto becomes more plausible.
Okay – I wasn’t clear enough in my earlier comment. I didn’t mean to suggest that you could get a good fit of a Pareto distribution to the batting average data for these 145 batters. The reason however, is not the fact that batting average is bounded [0,1] – rather, it’s because the distribution of batting averages is *nowhere close* to Pareto.
DeleteI’ll try another tack. Take a variable – U.S. annual individual income – that is plausibly Pareto distributed (I don’t have data to prove this, but anecdotally it is – so work with me). Let’s also assume minimum income is zero (or just eliminate from the analysis those with negative incomes). Now, find the individual who has the maximum income. Say it’s Warren Buffett (it probably isn’t, but I don’t want to think it’s an entertainer, a professional athlete, or a hedge fund manager, and Mr. Buffett seems to be a nice guy – plus, if I picked Bill Gates, you’d delete my comment).
Now, create a new variable – Income as a Proportion of Warren’s (IPOW) – by dividing every individual’s income by Mr. Buffett’s. This strikes me as a worthwhile performance measure, worthy of maximizing. [“Well Professor Rubin, we appreciate your interest in joining our country club, and your handicap (being a Cowboys fan) is acceptable – but we’d really like to see a little higher IPOW.”]
IPOW, of course, is bounded [0,1] – but I’ll bet it’s still Pareto distributed.
Now, if we looked at a “productivity” measure – income per unit of effort expended – we might see something more like a normal distribution (and the club might welcome you with open arms and offer you Warren’s locker). ;-)
There's a problem or two with the IPOW analogy, but they're not really central here. You can always scrunch a positive (right) skewed distribution into a [0, 1] interval with acceptable probability of predicting the impossible (value > 1); it's a question of whether that fit crams so much mass at the low end that it would make it unusable as a performance scale (the context of the paper).
DeleteI experimented a bit with a Pareto for the MLB batting average, using the Mendoza line (0.200) as the minimum and allowing Pr(BA > 1) to be around 0.001 (which I think is a bit generous, given the number of major leaguers). Note that this was NOT a fit to the actual data, just a theoretical distribution given those constraints. It gives a reasonably plausible mean BA around 0.261 and a somewhat less plausible median of 0.235. The first quartile is a somewhat implausible 0.214 (can you picture 1/4 of position players hitting that low, charitably counting the DH as a position?), and the probability of batting 0.400 or better is a bit over 0.05, which clearly does not fit historical data. The main issue, though, is whether (min, Q1, Q2) = (0.200, 0.214, 0.235) would distinguish enough among the bottom half of all hitters that someone would find the scale useful to measure hitting ability. I'm skeptical, but it's not as bad as my intuition (when I said BA _couldn't_ be Pareto would have had it.
Still, I think there's not much chance historical data could have fit a Pareto given the [0, 1] limit and the presumption that averages in the lower half would spread out "reasonably". I'm willing to believe that the data fits a normal (meaning I'm too lazy to check). That still leaves the possibility of a different distribution with right skew (but a less extreme tail) also fitting the sample.
Or maybe the authors argument really does just apply to performance measures where there's no obvious hard-and-fast upper limit.
Apologies in advance for any naivety and tardiness (asynchronous communication is quirky). I wonder if both distributions may be in play in the batting average example. I imagine that the population of batters come from the 20% group of a Pareto distribution of the all candidates (those of us in the 80% on the playground knew who the 20% were). The skill set of that 20% is perhaps a Gaussian distribution albeit one that is actively being culled with by the baseball farm system (tiered leagues) with lower performers being culled out of the system and higher performers being promoted (lather, rinse, repeat). All the populations will have been manipulated to some extent - even the baseball players vs non-baseball players, it is dependent on unarticulated assumptions.
ReplyDeleteI can't rule out what you are saying, but the playground part may be key here. If we're talking about a Pareto distribution for batting ability, then the vast majority of the kids on the playground would fit into the category I was in, which the late Tommy Lasorda accurately characterized as "couldn't hit water falling out of a boat". My recollection, however, is that the bulk of the kids (at least in gym class) were so-so, not good enough to make the school team but also not flailing away like me. So while I agree with the 20% (ish) quota for serious jocks, I'm skeptical that the density function of the other 80% would look like a Pareto density.
Delete