User Cuts versus Lazy Constraints

After an e-mail exchange with a contact at IBM, I recently gained a bit of clarity (I hope) about the distinction between user cuts and lazy constraints in CPLEX, which I will share here. The terminology and some of the details in this post are specific to CPLEX, but I suspect that a number of other solvers will have something analogous to user cuts and lazy constraints, albeit perhaps under different names. If the terminology is familiar to you, you can skip to the end of the post and find the one potentially useful nugget of information it contains.

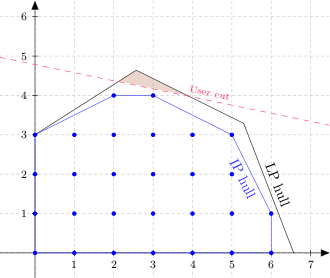
Let me start with an illustration of the feasible region of a hypothetical two variable pure integer linear program.

The polygon bounded in black (including portions of the two axes) is the feasible region of the linear program relaxation (also known as the linear hull or LP hull). This is what you get if you relax the integrality restrictions while enforcing all functional constraints and variable bounds. The blue dots are the integer lattice points inside the polygon, i.e., the feasible solutions that meet the integrality restrictions. The blue polygon, the integer hull or IP hull, is the smallest convex set containing all integer-feasible solutions. The IP hull is always a subset of the LP hull. Assuming a linear objective function, one of the vertices of the IP hull (all of which are lattice points) will be the optimal solution to the problem.

User Cuts

In CPLEX parlance, a cut is a constraint that is not part of the original model and does not eliminate any feasible integer solutions. Cuts are typically added for one of two reasons: to separate a node in the search tree into two nodes representing smaller subproblems; or to strengthen bounds by paring away some of the fat in the LP hull (the "fat" being the set difference between the LP hull and the IP hull). CPLEX automatically adds a variety of cuts, of which the most famous is arguably the Gomory cut. A user cut is simply a cut added by the user, rather than by CPLEX, frequently but not necessarily inside a callback. The next figure illustrates a user cut (red dashed line).

The shaded triangle shows the portion of the original LP hull that is removed by the user cut. Note that no integer solutions were harmed in the construction of this diagram.

Lazy Constraints

In contrast to user cuts, lazy constraints are allowed to pare away integer-feasible solutions. The next figure shows an example of a lazy constraint (green line).

The shaded polygon is again the portion of the LP (and, in part, IP) hull removed by the constraint. Note that, this time, three integer points are being rendered infeasible. The implication of using lazy constraints is that the problem originally specified (first figure) is actually a relaxation of the true problem; adding the lazy constraints to that initial problem gives you the problem you really want to solve.

Why use lazy constraints? Three reasons come to mind. First, a full specification of the model may involve an extremely large number of constraints, many of which you anticipate will be redundant, or at least not binding near the optimal solution. If you knew in advance which of those constraints were redundant, you could simply omit them, but frequently you cannot identify redundant constraints at the outset. Many modern solvers allow you to put a portion of the constraints (what we are calling the "lazy" ones) in a pool, where they are initially not a part of the active model. As solutions are generated, the solver checks to see if any lazy constraints are violated and, if so, adds them to the active set. Lazy constraints that were previously added but have not been binding for a while may be returned to the pool. This is an attempt to reduce the computation time per iteration, and possibly the memory footprint of the problem.

A second and closely related reason to use lazy constraints is that there may in fact be so many constraints that you cannot afford the time or memory to generate them all at the outset. One approach to formulating the Traveling Salesman Problem as an integer program requires the use of subtour elimination constraints. The number of such constraints grows exponentially with the number of nodes in the network. While they are easy to specify in a computer program, for decent size networks you simply cannot afford to list them all. An alternative is to treat them as lazy constraints and generate them on the fly, through a callback.

The third reason to use lazy constraints, specifically in a callback, is that you may not be able to identify them at the time the model is specified. The feasibility and optimality cuts generated during Benders decomposition fall into this category. You discover them by solving one or more subproblems at certain points in the search for the solution to the master problem.

Why Two Categories?

We've observed that the distinction between user cuts and lazy constraints is fundamentally whether or not they can cut off otherwise feasible solutions. The reason we care about that is somewhat arcane. CPLEX and other solvers do a variety of problem reductions, both at the outset (presolving) and on the fly during the search process, to tighten the feasible regions of node problems and expedite the solution process. Some of those reductions involve solutions to dual problems. User cuts do not affect the reductions, but if you hide some actual constraints in a pool of lazy constraints (or generate them after the reductions have been done), the dual solutions used in the reductions are incomplete (lacking dual variables corresponding to the constraints that are not yet included). This can lead to incorrect results.

If CPLEX sees the user adding lazy constraints (or, by virtue of the presence of a lazy constraint callback, threatening to add lazy constraints), it automatically turns of reductions that might be incorrect. I recently ran a program that uses CPLEX (12.4) with a lazy constraint callback. The output contained the following message:

Lazy constraint(s) or lazy constraint callback is present.
    Disabling dual reductions (CPX_PARAM_REDUCE) in presolve.
    Disabling non-linear reductions (CPX_PARAM_PRELINEAR) in presolve.

As user, you can turn off these reductions manually, but including a lazy constraint callback (or adding constraints to the lazy constraint pool during model construction) will induce CPLEX to do it for you.

So What Got Clarified?

A few versions ago, IBM refactored their implementation of cut callbacks. Of particular interest is the conditions under which cut callbacks are called.

• User cuts may be checked and applied at any time during the optimization process. This includes the cut generation phase at each node. They are not guaranteed to be checked at the time a candidate solution (potential new incumbent) is found, however. Calling a constraint a user cut tells CPLEX that it cannot cut off a feasible solution, so there is no need to test it each time a feasible solution is found.
• Lazy constraints, on the other hand, are guaranteed to be checked each time CPLEX finds a candidate solution, regardless of how the candidate is found (node LP solution, rounding, various heuristics, inferred from the position of the planets ...). This is important, because a lazy constraint might make the candidate solution infeasible in the full problem. (There is one small exception, at least as of version 12.4 and earlier: a candidate solution injected by the user through a heuristic callback is not checked against the lazy constraints. The user is somewhat charitably assumed to know what she or he is doing, so a user-injected solution is assumed to satisfy all lazy constraints.) What changed in the refactoring of the cut callback interface is that lazy constraints are checked only when a candidate solution is found. They are not routinely checked at every node.

I mainly use lazy constraints in Benders decomposition, and I generate Benders cuts only when a new incumbent is proposed, so this is fine with me. Discussions on various CPLEX and OR forums tells me that other people doing Benders sometimes want to check for possible Benders cuts at every node. There may be other scenarios unknown to me where users desire to check lazy constraints at each node. Before the refactoring, this was possible, but the new rule that lazy constraint callbacks are called only when potential incumbents are identified seems to throw up an obstacle. This is compounded by the fact that the current CPLEX documentation threatens the user with exile to the Phantom Zone should she or he dare lie and call a lazy constraint a user cut.

So here, at last, is the clarification. It turns out that it is legal to add a lazy constraint in a user cut callback (gasp!) as long as the user includes a lazy constraint callback or otherwise ensures that the necessary reductions are turned off. Since user cut callbacks are not called when candidate incumbents are found, at least for Benders decomposition this would suggest adding the same cut generation logic in both a lazy constraint callback (mandatory) and a user cut callback (optional).

I'm told that the next (?) release of official documentation for CPLEX will include this clarification. To close, I'll note that if you intend to sneak lazy constraints into a user cut callback, the safest way to do this may be to include a lazy constraint callback, even if it does nothing (just returns with no action). That way, CPLEX will automatically turn off everything that needs to be turned off. As I said, you can use parameter settings to turn off reductions manually, but which reductions will need to be turned off could potentially change in a new version. I, for one, am too lazy (pun deliberate) to keep up with that stuff.