Brace yourself (or flee now) -- this is a rather long post.
Introduction
IBM has announced the next version of CPLEX Studio (20.1), with planned availability around December 11, 2020. As to why the version number is jumping from 12.10 to 20.1, I have no idea ... but this is 2020, and I have no explanation for pretty much everything that has happened this year.
Among the changes in version 20.1, they have added a new value to the MIP emphasis parameter. Prior to 20.1, there were five possible values for the emphasis parameter:
- 0 = Balance optimality and feasibility(default)
- 1 = Emphasize feasibility
- 2 = Emphasize proven optimality
- 3 = Emphasize improving the best bound
- 4 = Emphasize finding "hidden" feasible solutions.
They have added the following new value:
- 5 = Emphasize heuristics (what Xavier Nodet calls "heuristics on steroids").
The motivation for this is fairly clear: commercial (i.e., paying) customers with difficulty MIP models are frequently less concerned about provable optimality than with getting the best solution they can find within some limited amount of run time. Exactly how the new setting differs from setting 4 (and, for that matter, how setting 4 differs from setting 1) is unclear to me, which is OK. (I'm worried that if I really understood all the nuances, my brain would explode.)
I've been part of the beta test program for 20.1, and I've tried the new setting on a few MIP models. Going in, I expected it to slow down throughput (the number of nodes digested per minute), since running lots of heuristics means spending more time at a typical node. The question is whether the extra time per node pays for itself by reducing sufficiently the number of nodes required to find a solution of a specified quality.
My first attempt was on a difficult problem that arose in some recently published research, and on that problem the setting was definitely not helpful. In fairness, though, there may be a good reason for that. The solution approach involves a variant of Benders decomposition, so the extra time spent on heuristics will frequently produce a "good" solution only to see it shot down by the subproblem (producing a feasibility cut violated by the solution). So the remainder of my tests were on MIP models that did not involve decomposition.
Test case 1: Partition
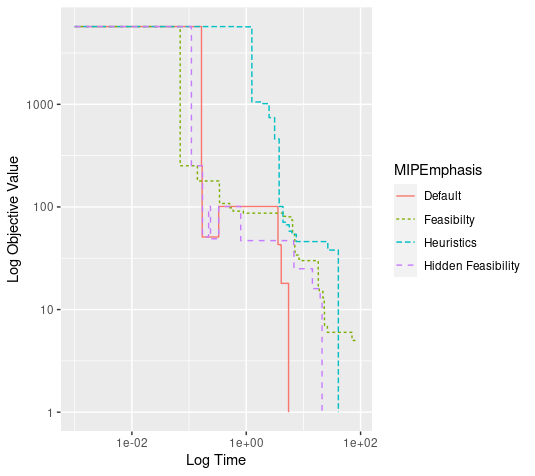
The first test case is a MIP model that glues together sets to minimize the range of set sizes in a partition of a master set. It was originally posted here in August, 2020. The test problem is actually quite easy to solve, with an optimal value of 1 (meaning the cardinalities of the sets formed differ by at most 1).
I ran the problem with a 90 second time limit (irrelevant in most cases), using each of the emphasis settings 0, 1, 4 and 5. The following plot (a log-log plot to enhance readability) shows the progress under each setting.
MIPEmphasis 1 ("Feasibility") makes the earliest progress but does not reach the optimal value of 1 within 90 seconds. (At that point, the incumbent value is 5.) Although just shy of one second some of the other levels do a little better than default, overall the default setting reaches the optimal solution fastest and the new setting is worse than the "Hidden Feasibility" setting. We can check the time at which each run (other than with emphasis 1) finds the optimal solution to confirm this.
MIPEmphasis | Time | |
|---|---|---|
| Default | 5.50 | |
| Hidden Feasibility | 21.19 | |
| Heuristics | 40.85 |
Test case 2: Typewriter
The second test case is a MIP model for laying out the keyboard of a hypothetical 19th century typewriter. The problem was featured in a series of posts, and the model used here appeared in the last of those posts. As I noted in that post, I was unable to find a provably optimal solution in large part due to a slow moving best bound, so for this demonstration I set a 60 second run limit. The problem seeks to minimize a distance measure. Once again, I'll use a log-log plot to show progress.
All the emphasis settings produce a rapid reduction in the objective function early on. After about a second or so, emphasis 1 (feasibility) seems to do a bit better than the others. Settings 4 and 5 seem to lag a bit. Looking at the final objective values (at the 60 second cutoff), however, it seems that setting 4 (hidden feasibility) did best, and setting 5 (heuristics) slightly outperformed the other settings.
MIPEmphasis | Best |
|---|---|
| Default | 5650882 |
| Feasibilty | 5660625 |
| Heuristics | 5640159 |
| Hidden Feasibility | 5517363 |
We can also look at node throughput. As a general rule, we would expect that increased use of heuristics would slow down node throughput. One possible exception would be settings that encouraged "diving" (local depth-first search), which might speed up processing of nodes during a dive.
The "heuristics" and "hidden feasibility" settings do in fact process fewer nodes in 60 seconds than does the default setting. The "feasibility" setting process about twice as many nodes as does the default setting, which may mean it does a fair bit of diving.
Test case 3: Group Selection
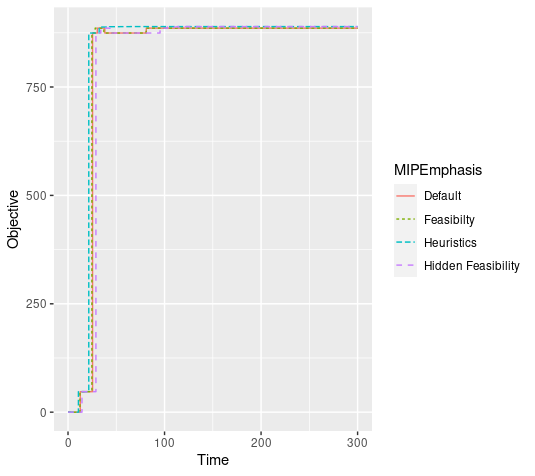
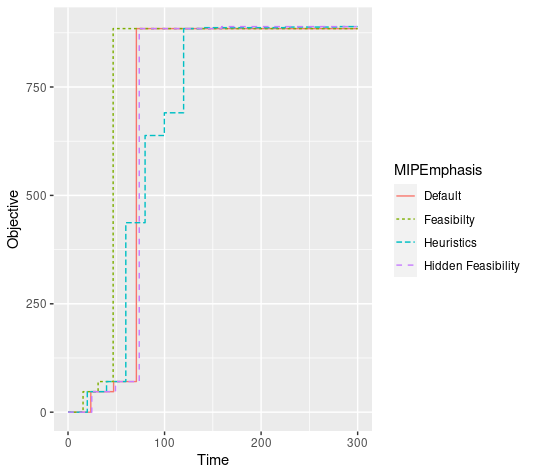
The last example is a group selection problem from yet another earlier post. I tested two slightly different MIP models with five minute time limits. The first variant uses continuous variables for some inherently boolean quantities, while the second variant makes those variables explicitly integer-valued. The second variant seems to be a bit harder to solve, even though they are mathematically equivalent.
The problem is a maximization problem, and none of the runs come remotely near proof of optimality. As noted in the earlier post, nonlinear approaches yielded an objective value of 889.3463, which is apparently optimal.
Looking at progress in the incumbent value, we see that all methods make substantial progress at the root node but shortly after the root node appear to bog down. In the first model, there is not much difference among the emphasis settings.
In the second model, the feasibility setting is a bit faster than the other to reach its maximum, and the heuristics setting is slower.
In both cases, though, the new "heuristics" setting produces the best objective value after 300 seconds.
MIPEmphasis | Best |
|---|---|
| Default | 885.7781 |
| Feasibilty | 885.7781 |
| Heuristics | 889.3451 |
| Hidden Feasibility | 889.3130 |
MIPEmphasis | Best |
|---|---|
| Default | 884.6917 |
| Feasibilty | 884.6917 |
| Heuristics | 889.3392 |
| Hidden Feasibility | 889.3130 |
As for node throughput, the next two plots show that node throughput is clearly greater in the first variant (where inherently boolean variables are treated a continuous with domain [0, 1]), and the "feasibility" setting is again fastest in both variants, while the new "heuristics" setting is slowest.
Conclusion
Testing on a small set of examples does not tell us much. On the group selection models, where progress is hard to come by after a short time, the new setting produced the best results, but was not much better than the old "hidden feasibility" setting. The same was true on the typewriter problem. So I am still waiting to encounter a problem instance where the new setting will provide a substantial improvement.




No comments:
Post a Comment
Due to intermittent spamming, comments are being moderated. If this is your first time commenting on the blog, please read the Ground Rules for Comments. In particular, if you want to ask an operations research-related question not relevant to this post, consider asking it on Operations Research Stack Exchange.