Decision diagrams, and in particular binary decision diagrams (BDDs) [1], were originally introduced in computer science to evaluate logic propositions or boolean functions. Lately, they've taken on multiple roles in discrete optimization [2]. I've been reading an excellent book [3] on them, with ideas about using BDDs in a current research project. As is my wont, I'll be coding the research in Java, so I wanted to do a little demo project to figure out how to build and process a BDD in Java.
Not wanting to reinvent any wheels, I looked for an open-source Java graph library with which to build the diagrams, and settled on JGraphT [4]. Not only does JGraphT have the necessary building blocks, it has much better online documentation than many libraries. Also, there is a very helpful article [5] about it on the Baeldung web site (which is itself an extremely useful site for all things Java).
A BDD is a directed, acyclic, layered multigraph with edge weights. If you're not familiar with the term "multigraph", it means that there can be two or more distinct edges between the same pair of nodes, in the same direction. In a BDD, each node represents a state of the system, with up to two outbound arcs, corresponding to true (1) or false (0) values for a particular decision variable. The decision variable is the same for all nodes in a particular layer. An arc is omitted if it represents a decision which, given the state, would make the solution infeasible. To keep the size of the BDD in check (somewhat), you do not want multiple nodes in a layer with the same state. The multigraph aspect arises because, in some circumstances, the next state may be the same regardless of the decision at the current node (so both arcs go to the same child node). Among the attractions of the JGraphT library are its support for nodes based on arbitrary classes (which in a BDD means the state at the node) and for multigraphs.
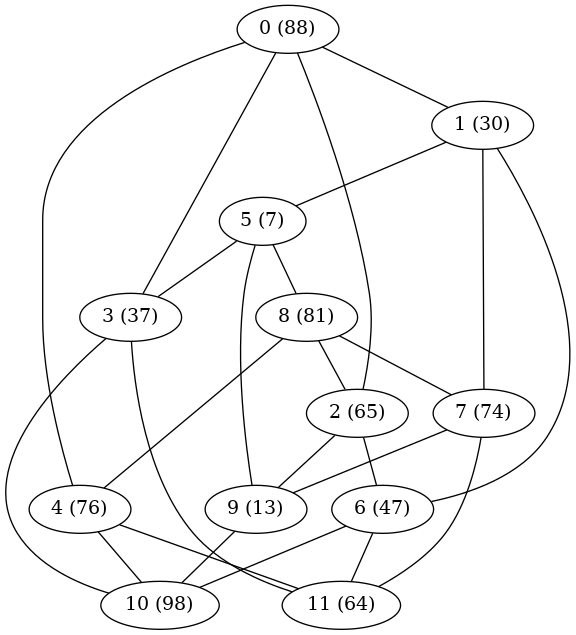
To learn how to build BDDs with JGraphT, I decided to solve a maximal independent set problem (MISP) [6] with integer node weights. This means choosing the subset of nodes with greatest total weight such that no two chosen nodes are adjacent. JGraphT contains routines to generate some well-known (to graph theorists -- less well known to me) graphs, and for convenience I chose the Chvátal graph [7], which has 12 nodes and 24 edges. Here is an illustration of the Chvátal graph, with the (randomly generated) node weights in parentheses.
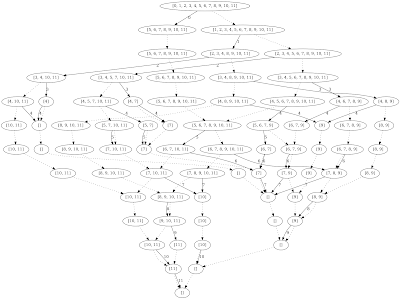
My Java program uses routines in the JGraphT library to turn the graph into a DOT file [8], which it saves. I then use GraphViz [9] outside the Java program to convert the DOT file into the format I need for wherever the plot is going.Using the same DOT export trick, I managed to generate a plot of the BDD, in which nodes display the set of vertices still available for addition to the independent set, arcs are solid if a vertex is being added to the independent and dotted if not, and solid arcs are annotated with the number of the vertex being added.
Unfortunately, Blogger does not accept SVG images and the BDD is a bit too big for a legible PNG graph. If you want to see a better image, click it and an SVG version should open in a new window or tab.This post is already a bit long, so I won't go into details about the various coding issues I ran into or how I worked around them. I will point out one minor mathematical issue. Since the MISP is a maximization problem, the goal is to find the longest (in terms of weight, not number of edges) path from root node to terminal node in the BDD. JGraphT has a package containing shortest path algorithms, but no longest path algorithms. Fortunately, the number of layers in the graph is fixed (one layer per decision variable, plus one to hold the terminal node), which means the number $L$ of links in a longest path is fixed. So we simply find the maximum weight $W$ of any node in the graph, change the weight $w_e$ of each edge $e$ to $LW - w_e$, and find the shortest path using the modified weights. That path is guaranteed to be the longest path with respect to the original weights.
Last thing: As usual, my code is available for you to play with from my GitLab repository.
No comments:
Post a Comment
Due to intermittent spamming, comments are being moderated. If this is your first time commenting on the blog, please read the Ground Rules for Comments. In particular, if you want to ask an operations research-related question not relevant to this post, consider asking it on Operations Research Stack Exchange.